Вступ до ієрархічного алгоритму кластеризації
Алгоритм ієрархічної кластеризації - це непідвладний метод машинного навчання. Він спрямований на пошук природного угрупування на основі характеристик даних.
Алгоритм ієрархічної кластеризації має на меті знайти вкладені групи даних шляхом побудови ієрархії. Це схоже на біологічну систематику рослинного чи тваринного царства. Ієрархічні кластери зазвичай представлені за допомогою ієрархічного дерева, відомого як дендрограма.
Типи ієрархічного алгоритму кластеризації
Алгоритми ієрархічної кластеризації мають два типи:
- Роздільний
- Агломеративні
1. Роздільний
Це підхід зверху вниз, де він спочатку розглядає всі дані як одну групу, а потім ітеративно розбиває дані на підгрупи. Якщо число алгоритму ієрархічної кластеризації відомо, то процес поділу припиняється, як тільки буде досягнуто кількість кластерів. Крім того, процес зупиняється, коли дані не можуть бути більше розділеними, а це означає, що підгрупа, отримана за допомогою поточної ітерації, така ж, як та, отримана з попередньої ітерації (також можна врахувати, що поділ припиняється, коли кожна точка даних є кластером ).
2. Агломеративний
Це підхід знизу вгору, який спирається на об'єднання кластерів. Спочатку дані розбиваються на m однотонних кластерів (де значення m - кількість вибірок / точок даних). Два кластери об'єднуються в один ітераційно, таким чином зменшуючи кількість кластерів за кожну ітерацію. Цей процес об'єднання кластерів припиняється, коли всі кластери були об'єднані в один або досягається кількість бажаних кластерів.
На рівні 1 є кластери m, які зменшуються до 1 кластера на рівні m. Ті точки даних, які об'єднуються і утворюють кластер на нижчому рівні, залишаються в тому самому кластері і на вищих рівнях. Наприклад, припустимо, що існує 8 балів x1..x8, тому спочатку на кластері є 8 кластерів. Припустимо, точки x1 і x2 об'єднуються в кластер на рівні 2, потім до рівня 8 вони залишаються в одному кластері.
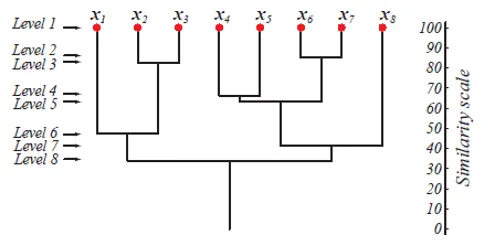
Наведений малюнок демонструє дендрограмне представлення кластеризації агломерації для 8 точок даних, а також шкалу подібності, що відповідає кожному рівню.
Рівні кластерів дають нам уявлення про те, наскільки схожі точки даних у кластерах. Як показано на фіг.1, чим раніше точки даних об'єднуються в кластер, тим вони схожі. Отже, точки даних у кластері на рівні 2 (наприклад, x2 та x3) схожіші, ніж точки даних у кластері на рівні 6 (наприклад, x1 та x2).
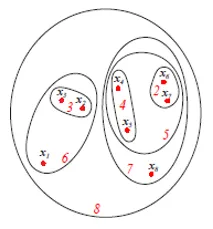
На наведеному малюнку зображено набір діаграм Set або Venn агломераційного підходу кластеризації вищезгаданих 8 точок даних. Для кластеризації можна використовувати як дендрограми, так і задані подання. Однак, як правило, дендрограма, бажано представлення активів, не може кількісно представити схожість кластеру.
Кроки до алгоритму ієрархічної кластеризації
Виконаймо наступні кроки для алгоритму ієрархічної кластеризації, які наведені нижче:
1. Алгоритм
Алгоритм агломераційного ієрархічного кластеризації
- Почніть ініціалізацію c, c1 = n, Di = (xi), i = 1, …, n '
- У c1 = c1 - 1
- Знайдіть найближчі кластери, скажімо, Di та Dj
- Об’єднайте Ді та Dj
- Доки c = c1
- Повернути кластери c
- Кінець
Цей алгоритм починається з n кластерів спочатку, де кожна точка даних є кластером. З кожною ітерацією кількість кластерів зменшується на 1, коли два найближчих кластери об'єднуються. Цей процес триває, поки кількість кластерів не зменшиться до заздалегідь заданого значення c.
Як визначити, які кластери знаходяться поруч?
Це визначається за допомогою декількох показників відстані, які є наступними:
- Мінімальна відстань між кластерами dmin (Di, Dj). Корисно для одиноких.
- Максимальна відстань між кластерами dmax (Di, Dj). Корисна для завершення.
- Середня відстань між кластерами davg (Di, Dj).
Що таке одинарна та повна зв'язки?
- Коли dmin (di, dj) використовується для знаходження відстані між двома кластерами, і алгоритм припиняється, якщо відстань між найближчими кластерами перевищує поріг, то алгоритм називається алгоритмом єдиного зв'язку.
- Коли dmax (Di, Dj) використовується для знаходження відстані між двома кластерами, і алгоритм припиняється, якщо відстань між найближчими кластерами перевищує поріг, то алгоритм називається повним алгоритмом зв'язку.
- Розглянемо кожну точку даних як вузол графіка. Існує край між двома точками даних, якщо вони належать до одного кластеру. Коли два найближчих кластери об'єднані, додається край. Його називають єдиним зв’язком, оскільки існує унікальний шлях від одного вузла до іншого.
- Алгоритм повного зв’язку об'єднує два кластери, мінімізуючи відстань між двома найдальшіми точками.
- Один алгоритм зв’язку генерує дерево, що охоплює. Однак цей алгоритм сприйнятливий до шуму. Повний алгоритм зв’язку генерує повний графік.
Яка часова складність алгоритму?
Припустимо, у нас є n візерунків у двовимірному просторі, і ми використовуємо dmin (Di, Dj) для формування c кластерів. Нам потрібно обчислити n (n - 1) міжточкових відстаней - кожне з яких є розрахунком O (d 2 ) - і розмістити результати в міжточковій таблиці відстаней. Складність простору дорівнює O (n 2 ). Пошук пари мінімальної відстані (для першого злиття) вимагає пройти повний список, зберігаючи індекс найменшої відстані.
Таким чином, для першого кроку агломерації складність становить O (n (n - 1) (d 2 + 1)) = O (n 2 d 2 ). Для іншого довільного кроку агломерації (тобто від c1 до c1 - 1) ми просто переходимо через n (n - 1) - c1 "невикористані" відстані у списку і знаходимо найменший, для якого x і x 'лежать в різних кластерах . Це знову ж таки O (n (n − 1) −c1). Таким чином, загальна часова складність становить O (cn 2 d 2 ), а в типових умовах n >> c.
2. Візуалізація
Після розподілу даних на кластери є доброю практикою візуалізації кластерів, щоб отримати уявлення про те, як виглядає групування. Але візуалізувати ці високомірні дані складно. Отже, ми використовуємо аналіз основних компонентів (PCA) для візуалізації. Після PCA ми отримуємо точки даних у просторі з низькими розмірами (як правило, 2D або 3D), які ми можемо побудувати, щоб побачити групування.
Примітка: високий розмір означає велику кількість функцій, а не кількість точок даних.3. Оцінка
Один із методів оцінки кластерів полягає в тому, що відстань точок між кластерами (міжкластерна відстань) повинна бути значно більшою, ніж відстань точок всередині кластера (внутрішньокластерна відстань).
Висновок
Нижче наведено кілька ключових заходів:
- Алгоритм ієрархічної кластеризації використовується для пошуку вкладених шаблонів у даних
- Ієрархічна кластеризація буває 2-х типів - подільна та агломераційна
- Для представлення можна використовувати дендрограму та діаграму set / Venn
- Одне з'єднання об'єднує два кластери, мінімізуючи мінімальну відстань між ними. Він утворює розтягування
- Повна зв'язок об'єднує два кластери, зводячи до мінімуму максимальну відстань між Воно утворює повний графік.
- Загальна часова складність алгоритму ієрархічної кластеризації становить O (cn 2 d 2 ), де c - заздалегідь визначена кількість кластерів, n - кількість шаблонів і d - розмірний простір n візерунків.
Рекомендовані статті
Це посібник з алгоритму ієрархічної кластеризації. Тут ми обговорюємо типи та етапи алгоритмів ієрархічної кластеризації. Ви також можете переглянути наступні статті, щоб дізнатися більше -
- Ієрархічний аналіз кластеризації
- Ієрархічна кластеризація в R '
- Алгоритм кластеризації
- Що таке кластеризація в майнінгу даних?
- Ієрархічна кластеризація | Агломераційна та роздільна кластеризація
- Алгоритм C ++ | Приклади алгоритму С ++