Складні номери в MATLAB - Як генерувати складне число?

Вступ до складних чисел у MATLAB

Складні числа - це поєднання дійсних чисел і уявних чисел у вигляді p + qi, де p і q - дійсні числа, а i - уявне число. Уявне число визначається, де i є результатом рівняння a 2 = -1. Ми можемо використовувати i або j для позначення уявних одиниць. Оскільки складні числа використовуються в будь-яких математичних обчисленнях, а Matlab в основному використовується для виконання математичних обчислень. Отже, складні числа складають важливу частину навчання Матлаба.

Генерація складних чисел у MATLAB

Складні номери можна створити або оголосити в Matlab за допомогою функції «складних». Ми також можемо створити складні числа, знайшовши квадратний корінь будь-якого від’ємного числа. У Matlab ми можемо використовувати i або j для позначення уявної частини комплексного числа.

Приклади

X = 4 + 5i

Тут X - це складне число, яке містить 2 частини, тобто реальну та уявну частину. 4 - реальна частина, а 5 - уявна частина. Ми можемо знайти реальні та уявні частини за допомогою функцій в Matlab.

a = real (X) = 4 (це дає дійсну частину комплексного числа)
b = imag (X) = 5 (Це дає уявну частину комплексного числа)
комплекс (6, 7) = 6 + 7i (Ця функція використовується для створення комплексного числа)

Ми також можемо створити складні масиви в Matlab, які також можна оголосити за допомогою складних функцій.

a = комплекс (x, y)

Існують певні умови для x і y, яких слід дотримуватися, як x, а y не повинні бути одиничними чи подвійними. Складний скаляр може бути створений, якщо два входи мають скалярний характер, наприклад,

X = комплекс (5, 3)
X = 5, 0000 + 3 000 000i

Аналогічно, складний вектор може бути створений, якщо у нас є два входи як вектори.

X = uint8 ((4; 5; 6; 7));
Y = uint8 ((3; 5; 1; 2));
a = комплекс (X, Y)

4 + 3i

5 + 5i

6 + 1i

7 + 2i

Ми можемо створити складне число, що має лише один скаляр,

X = комплекс (10)
X = 10, 0000 + 0, 0000i

Існують певні умови, яким слід дотримуватися вхідних та вихідних аргументів,

Вхідні аргументи містять реальні та уявні частини, такі як x будь-який y. x і y мають бути скалярними, векторними, багатовимірними масивами або матрицями в MATLAB. розмір x і y має бути однаковим. Вони повинні бути одного типу даних, але є кілька винятків, як подвійний може використовуватися з одинарним, а ціле число може поєднуватися з подвійним, що є скалярним.

Вихід масиву може бути векторним, скалярним, матричним або багатовимірним масивом залежно від вхідних аргументів. Розмір виводу повинен бути таким же, як і вхід. Якщо вхідні аргументи мають різні типи даних, то вихід визначається,

Якщо будь-який з вхідних аргументів є єдиним за своєю суттю, то вихід також повинен бути одиничним.
Якщо будь-який з вхідних аргументів має ціле число, то вихід повинен мати цілий тип даних.

Ми можемо перевірити, чи є матриця реальною чи уявною, використовуючи функцію isreal.

Код:

X = (2+i, 1); Isreal(X)

Вихід:

Код:

Isreal (X (2))

Вихід:

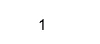
Щоб витягнути реальні та уявні частини, ми можемо використовувати реальні та функції зображень у Matlab,

Код:

real(X)

Вихід:

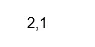
Код:

imag(X)

Вихід:

Операції та функції складних чисел у MATLAB

Існує кілька операцій і функцій, які можна виконати, використовуючи складні числа в Matlab

abs: Ця функція використовується для пошуку модуля будь-якого складного числа у вигляді p + qi. abs (2 + 3i) = квадратний корінь (2 2 + 3 2) = (13) 0, 5
кут: Для знаходження фазового кута комплексного числа.

Існують певні поради, яких слід дотримуватися для правильного функціонування складних чисел у Matlab, наприклад,

Ми повинні уникати використання i та j як частини будь-яких імен змінних, оскільки вони використовуються при позначенні уявних частин комплексного числа.
Ми повинні уникати використання j або i, якщо уявна частина дорівнює 1. Натомість ми можемо використовувати 1j або 1i.
Ми можемо створити складну функцію в Matlab, коли i і j в якійсь частині використовуються як імена змінних, вхідні аргументи не одинарного або подвійного типу, а уявна частина дорівнює нулю.

Висновок

Складні числа використовуються в математичній або інженерній галузі. Багато реальних або практичних застосувань можна описати, використовуючи уявну частину складних чисел. Отже, розуміння використання та застосування складних чисел на різних платформах важливо, особливо якщо ви маєте справу з будь-якою фізичною чи математичною областю.