Вступ до математичних функцій в C ++
Це важко і трудомістко, коли доводиться кожного разу писати код, щоб робити основні математичні обчислення у своїй програмі. Тому C ++ забезпечує величезну кількість математичних функцій, щоб зробити ваш код простим та ефективним. Ви можете робити велику кількість операцій над числами, використовуючи математичні функції. Оскільки ці функції вбудовані та підтримуються бібліотекою в C ++, тому необхідно включити файл заголовка або на початку коду, щоб використовувати всі функції математичних функцій. Не потрібно писати логіку в коді для виконання операцій, все це є в бібліотеці.
Різні типи математичних функцій
C ++ забезпечує величезну кількість різних типів математичних функцій, згаданих нижче, із прикладами:
1. Максимальна та мінімальна функції
- max (p, q): поверне максимальне число між p і q.
- min (p, q): поверне мінімальну кількість між p і q.
Код C ++ для реалізації вище функціональності
#include
#include
using namespace std;
int main() (
cout << max(16, 18) << "\n";
cout << min(16, 18) << "\n";
return 0;
)
Вихід:

2. Силові функції
- pow (m, n): Обчислить m, підняту до потужності n.
- sqrt (m): буде обчислено квадратний корінь m.
- cbrt (n): Він обчислить корінь куба n.
- hypot (m, n): Він обчислить гіпотенузу прямокутного трикутника.
Код C ++ для реалізації вищевказаної функціональності
#include
#include
using namespace std;
int main() (
cout << pow(2, 3) << "\n";
cout << sqrt(16) << "\n";
cout << cbrt(27) << "\n";
cout << hypot(3, 4) << "\n";
return 0;
)
Вихід:

3. Експоненціальні функції
- exp (p): Він обчислить експоненцію e, підняту до потужності p.
- log (p): Обчислить логарифм p.
- log10 (p): Обчислить загальний логарифм p.
- exp2 (p): Обчислить базову експоненцію p.
- log2 (p): Обчислить базовий 2 логарифм p.
- logb (p): Обчислить логарифм p.
Код C ++ для реалізації вищевказаної функціональності
#include
#include
using namespace std;
int main() (
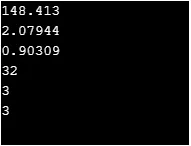
cout << exp(5) << "\n";
cout << log(8) << "\n";
cout << log10(8) << "\n";
cout << exp2(5) << "\n";
cout << log2(8) << "\n";
cout << logb(8) << "\n";
return 0;
)
Вихід:
4. Цілі функції
Це допомагає знайти найближче ціле значення.
- ceil (z): він округляє значення z.
- пол (z): він округляє значення z.
- круглий (z): він округляє значення z.
- fmod (z, y): він обчислює залишок ділення z / y.
- trunc (z): Він округлятиме значення z до нуля.
- rint (z): Він округлятиме значення z за допомогою режиму округлення.
- Nearint (z): Він округлятиме значення z до цілісного значення поблизу.
- залишок (z, y): він обчислить залишок z / y.
Код C ++ для реалізації вищевказаної функціональності
#include
#include
using namespace std;
int main() (
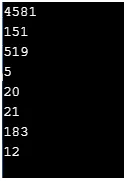
cout << ceil(4580.01) << "\n";
cout << floor(151.999) << "\n";
cout << round(518.5) << "\n";
cout << fmod(5, 21) << "\n";
cout << trunc(20.25) << "\n";
cout << rint(21.25) << "\n";
cout << nearbyint(182.55) << "\n";
cout << remainder(12, 36) << "\n";
return 0;
)
Вихід:
5. Функції порівняння
Допомога в порівнянні чисел за швидкий проміжок часу не має значення, скільки триває це число. Нижче наведено кілька прикладів функцій порівняння:
- вище (p, q): він перевіряє, чи p більше, ніж q чи ні.
- islessequal (p, q): він перевіряє, чи p менше або рівний q чи ні.
- isgreaterequal (p, q): він перевіряє, чи p більше чи дорівнює q чи ні.
- islessgreater (p, q): він перевіряє, чи p менший чи більший ніж y чи ні.
- невпорядкований (p, q): він перевіряє, порівняно чи ні р
Код C ++ для реалізації вищевказаної функціональності
#include
#include
using namespace std;
int main() (
// cout << less(22, 29) << "\n";
cout << isgreater(48, 47)<< "\n";
cout << islessequal(11, 5)<< "\n";
cout << isgreaterequal(19, 72)<< "\n";
cout << islessgreater(59, 84)<< "\n";
cout << isunordered(62, 84)<< "\n";
return 0;
)
Вихід:

6. Використання тригонометричної функції
Функції, спеціально використовувані в геометричних обчисленнях. Прямокутний трикутник дає відношення між кутом і відношенням довжини двох сторін.
- sin (y): Він обчислить значення синуса y.
- cos (y): Він обчислить значення косинуса y.
- tan (y): Обчислить значення дотичної y.
- asin (y): Він обчислить значення зворотного синуса y.
- acos (y): Обчислить значення зворотного косинуса y.
- atan (y): Обчислить значення оберненої дотичної y.
- atan2 (y, x): Обчислить значення оберненої дотичної координат y і x.
Код C ++ для реалізації вищевказаної функціональності
#include
#include
using namespace std;
int main() (
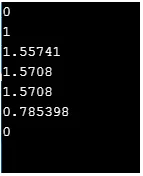
cout << sin(0) << "\n";
cout << cos(0) << "\n";
cout << tan(1) << "\n";
cout << asin(1)<< "\n";
cout << acos(0)<< "\n";
cout << atan(1)<< "\n";
cout << atan2(0, 1)<< "\n";
return 0;
)
Вихід:
Ось ще кілька цікавих функцій, які допоможуть обчислити значення гіперболічних тригонометричних функцій, і вони називаються гіперболічними функціями.
- sinh (x): Він обчислить значення гіперболічного синуса x.
- cosh (x): Він обчислить значення гіперболічного косинуса x.
- tanh (x): Обчислить значення гіперболічної дотичної точки x.
- asinh (x): Він обчислить значення синуса гіперболічної дуги x.
- acosh (x): Він обчислить значення гіперболічного дугового косинуса x.
- atanh (x): Він обчислить значення синуса гіперболічної дуги x.
Код C ++ для реалізації вищевказаної функціональності
#include
#include
using namespace std;
int main() (
cout << sinh(0)<< "\n";
cout << cosh(0)<< "\n";
cout << tanh(1)<< "\n";
cout << asinh(1)<< "\n";
cout << acosh(1)<< "\n";
cout << atanh(0)<< "\n";
return 0;
)
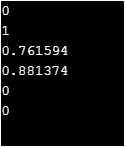
Вихід:
Висновок
Математичні функції відіграють важливу роль в економії величезної кількості часу та місця в пам'яті. Всі функції вбудовані, немає необхідності безпосередньо використовувати будь-яку математичну функцію, просто додавши файл заголовка, який дасть можливість використовувати всю бібліотеку математичного класу.
Рекомендовані статті
Це посібник з математичних функцій на C ++. Тут ми обговорюємо, що C ++ надає величезну кількість різних типів математичних функцій із прикладами. Ви також можете ознайомитися з іншими запропонованими нами статтями -
- Перевищення рівня C ++
- Перевантаження в C ++
- Квадратний корінь в C ++
- Масиви в C ++
- Перевантаження в Java
- Квадратний корінь в PHP
- Топ-11 особливостей та переваг C ++
- Керівництво по Square Root в JavaScript