Різниця між лінійною регресією та логістичною регресією
Наступна стаття Лінійна регресія проти логістичної регресії забезпечує найбільш важливі відмінності між обома, але перш ніж ми побачимо, що означає регресія?
Регресія
Регресія - це, в основному, статистичний показник для визначення сили зв'язку між однією залежною змінною, тобто виведенням Y, і рядом інших незалежних змінних, тобто X 1, X 2 тощо. Регресійний аналіз в основному використовується для прогнозування та прогнозування.
Що таке лінійна регресія?
Лінійна регресія - це алгоритм, який базується на контрольованій навчальній області машинного навчання. Він успадковує лінійну залежність між його вхідними змінними та єдиною вихідною змінною, де вихідна змінна має суцільний характер. Він використовується для прогнозування значення виходу, скажімо, Y з входів, скажімо, X. Якщо вважається лише один вхід, це називається простою лінійною регресією.
Його можна класифікувати на дві основні категорії:
1. Проста регресія
Принцип дії: Основна мета - знайти рівняння прямої, яка найкраще відповідає вибірковим даним. Це рівняння алгебраїчно описує зв'язок між двома змінними. Найпридатніша пряма називається регресійною лінією.
Y = β 0 + β 1 X
Де,
β представляє ознаки
β 0 являє собою перехоплення
β 1 являє собою коефіцієнт ознаки X
2. Багатовимірна регресія
Він використовується для прогнозування кореляції між більш ніж однією незалежною змінною та однією залежною змінною. Регресія з більш ніж двома незалежними змінними заснована на пристосуванні форми до сузір'я даних на багатовимірному графіку. Форма регресії повинна бути такою, щоб вона мінімізувала відстань фігури від кожної точки даних.
Модель лінійних відносин може бути представлена математично як нижче:
Y = β 0 + β 1 X 1 + β 2 X 2 + β 3 X 3 + ……. + β n X n
Де,
β представляє ознаки
β 0 являє собою перехоплення
β 1 являє собою коефіцієнт ознаки X 1
β n являє собою коефіцієнт ознаки X n
Переваги та недоліки лінійної регресії
Нижче наведено переваги та недоліки:
Переваги
- Завдяки своїй простоті він широко застосовується для моделювання прогнозів та умовиводів.
- Основна увага приділяється аналізу даних та попередній обробці даних. Отже, він має справу з різними даними, не турбуючись про деталі моделі.
Недоліки
- Він працює ефективно, коли дані нормально поширюються. Таким чином, для ефективного моделювання необхідно уникати колінеарності.
Що таке логістична регресія?
Це форма регресії, яка дозволяє передбачати дискретні змінні за допомогою суміші безперервних та дискретних предикторів. Це призводить до унікальної трансформації залежних змінних, яка впливає не тільки на процес оцінки, але і на коефіцієнти незалежних змінних. Він вирішує той самий питання, який має багаторазова регресія, але без розподільних припущень щодо прогнозів. У логістичній регресії змінна результат є двійковою. Мета аналізу полягає в оцінці ефектів декількох пояснювальних змінних, які можуть бути числовими, категоричними або обома.
Види логістичної регресії
Нижче наведено два типи логістичної регресії:
1. Двійкова логістична регресія
Він використовується, коли залежна змінна є дихотомічною, як дерево з двома гілками. Він використовується, коли залежна змінна є непараметричною.
Використовується коли
- Якщо немає лінійності
- Існує лише два рівні залежної змінної.
- Якщо багатоваріантна нормальність сумнівна.
2. Багаточленна логістична регресія
Мультиноміальний логістичний регресійний аналіз вимагає, щоб незалежні змінні були метричними або дихотомічними. Він не робить жодних припущень щодо лінійності, нормальності та однорідності дисперсії для незалежних змінних.
Він використовується, коли залежна змінна має більше двох категорій. Він використовується для аналізу зв’язків між неметричною залежною змінною та метричними чи дихотомічними незалежними змінними, а потім порівнює кілька груп за допомогою комбінації бінарних логістичних регресій. Зрештою, він надає набір коефіцієнтів для кожного з двох порівнянь. Коефіцієнти для референтної групи приймаються за всі нулі. Нарешті, прогнозування робиться на основі найбільшої ймовірності в результаті.
Перевага логістичної регресії: Це дуже ефективна і широко застосовувана методика, оскільки не потребує багатьох обчислювальних ресурсів і не потребує налаштування.
Недолік логістичної регресії: її не можна використовувати для вирішення нелінійних задач.
Порівняння «лінійка до голови» між лінійною регресією та логістичною регресією (Інфографіка)
Нижче наведено найкращі 6 відмінностей між лінійною регресією та логістичною регресією 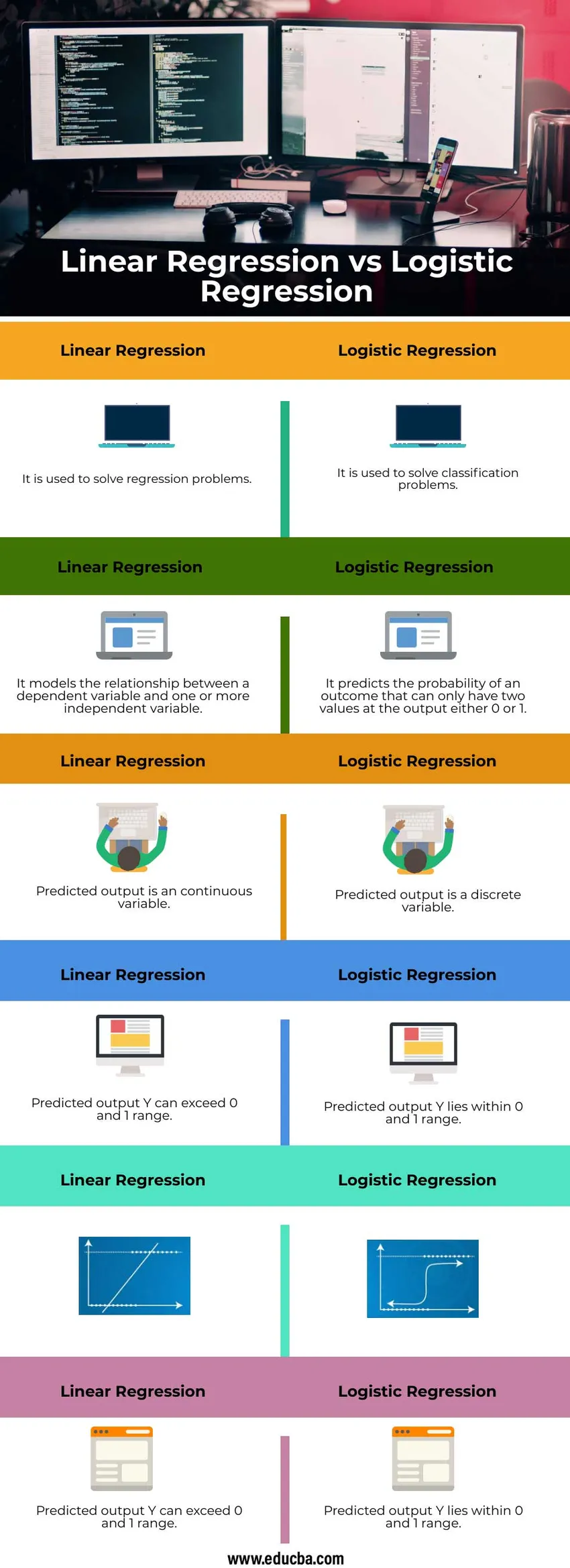
Ключова різниця між лінійною регресією та логістичною регресією
Давайте обговоримо деякі основні відмінності між лінійною регресією та логістичною регресією
Лінійна регресія
- Це лінійний підхід
- Тут використовується пряма лінія
- Він не може приймати категоричні змінні
- Він повинен ігнорувати спостереження з пропущеними значеннями числової незалежної змінної
- Вихід Y задається як
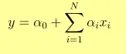
- 1 одиниця збільшення x збільшує Y на α
Програми
- Прогнозування ціни товару
- Прогнозування рахунку в матчі
Логістична регресія
- Це статистичний підхід
- Тут використовується сигмоподібна функція
- Він може приймати категоричні змінні
- Він може приймати рішення, навіть якщо є спостереження з відсутніми значеннями
- Вихід Y задається як, де z задано як
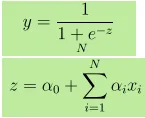
- Зростання на 1 одиницю x збільшує Y за коефіцієнта log α
- Якщо P - вірогідність події, то (1-P) - це ймовірність того, що вона не відбудеться. Шанси на успіх = P / 1-P
Програми
- Прогнозуючи, буде сьогодні дощ чи ні.
- Прогнозування того, електронний лист є спамом чи ні.
Таблиця порівняння лінійної регресії проти логістичної регресії
Давайте обговоримо найкраще порівняння між лінійною регресією та логістичною регресією
|
Лінійна регресія |
Логістична регресія |
| Він використовується для вирішення проблем регресії | Він використовується для вирішення задач класифікації |
| Він моделює взаємозв'язок між залежною змінною та однією або декількома незалежними змінними | Він прогнозує ймовірність результату, який може мати лише два значення на виході або 0, або 1 |
| Прогнозований вихід є суцільною змінною | Прогнозований вихід - дискретна змінна |
| Прогнозований вихід Y може перевищувати 0 та 1 діапазон | Прогнозований вихід Y лежить в межах 0 і 1 діапазону |
 | 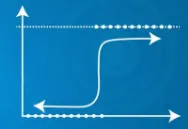 |
| Прогнозований вихід Y може перевищувати 0 та 1 діапазон | Прогнозований вихід |
Висновок
Якщо функції не сприяють передбаченню або вони дуже сильно співвідносяться між собою, то це додає шуму моделі. Отже, функції, які недостатньо сприяють моделі, повинні бути видалені. Якщо незалежні змінні сильно корелюються, це може спричинити проблему мультиколінеарності, яку можна вирішити, запустивши окремі моделі з кожною незалежною змінною.
Рекомендовані статті
Це керівництво щодо лінійної регресії проти логістичної регресії. Тут ми обговорюємо ключові відмінності лінійної регресії проти логістичної регресії за допомогою інфографіки та таблиці порівняння. Ви також можете переглянути наступні статті, щоб дізнатися більше -
- Data Science vs Візуалізація даних
- Машинне навчання проти нейронної мережі
- Контрольоване навчання проти глибокого навчання
- Логістична регресія в R