Вступ до сортування купи в С
Сортування - це техніка, яка полягає у впорядкуванні елементів на основі різних властивостей. (Такі властивості, як упорядкування даних у порядку зростання, спадання чи в алфавітному порядку). Одним з головних прикладів сортування, про які ми можемо придумати, є замовлення товарів під час покупки в Інтернеті. Ми можемо пов'язати з цінами, популярністю, найновішими тощо. Тож існує багато прийомів такого розміщення елементів за допомогою сортування. У цій темі ми дізнаємось про сортування купи в C.
Тут ми вивчимо одну з найпоширеніших методів сортування, сортування Heap, через мову програмування C.
Логіка сортування купи
Як насправді ми можемо виконувати сортування купи? Давайте перевіримо нижче.
По-перше, купа є однією з деревних даних. Дерево, яке тут бере участь, - це завжди Повне Бінарне Дерево. І, існує два види купи
- Min - Heap: загалом розташовані у порядку зростання, тобто якщо елемент батьківського вузла має значення, менше, ніж у дочірніх елементів вузла.
- Max - Heap: загалом розташований у порядку зменшення, тобто якщо елемент батьківського вузла має значення більше, ніж значення дочірніх елементів вузла.
Кроки для сортування купи
- Після отримання несортованих даних списку елементи впорядковуються в структурі даних купи або засновані на створенні min-heap або max-heap.
- Перший елемент із наведеного списку додається до нашого масиву
- Знову формується техніка структури даних голови, як і перший крок, і знову або найвищий елемент, або найменший елемент підбирається і додається до нашого масиву.
- Повторні кроки допомагають нам отримати масив із відсортованим списком.
Програма для сортування купи в С
#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)
По-перше, ми просимо користувача ввести кількість елементів, взятих для сортування, а потім користувачеві дозволяється вводити різні елементи, які потрібно сортувати.
Виконані кроки
- Наступним, на якому ми зосереджуємось, є створення масиву купи, в даному випадку масиву max-heap.
- Основна умова для отримання масиву max - купи - перевірити, чи не має значення батьківського вузла менше його дочірнього значення вузла. Ми збираємось обмінятися, поки не досягнемо цієї умови.
- Основна перевага цього повного двійкового дерева полягає в тому, що лівий і правий дочірні вузли батьківського вузла можуть отримати доступ зі значеннями 2 (i) + 1 та 2 * (i) + 2 відповідно. Де я - батьківський вузол.
- Отже, таким чином тут ми розміщуємо наш кореневий вузол, який містить максимальне значення у правому правому місці листового вузла. А потім знову слідуючи тій же процедурі, що наступне максимальне число тепер стає кореневим вузлом.
- Ми будемо виконувати ту саму процедуру, поки в масиві купи не залишиться лише один вузол.
- Потім ми організовуємо наш масив для формування ідеального відсортованого масиву в порядку збільшення.
- Нарешті, ми друкуємо відсортований масив у висновку.
Вихід:
Вихід додається нижче.
Дозвольте показати вам мальовниче зображення подій:
- Введені дані спочатку представляються у вигляді одновимірного масиву наступним чином.

- Мальовниче зображення сформованого бінарного дерева таке:
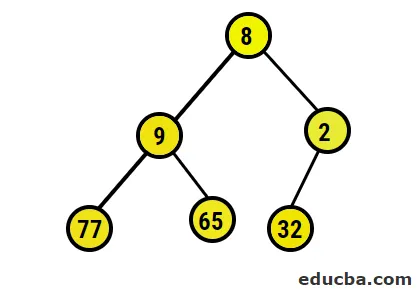
- Тепер ми переходимо до максимальної купи, переконуючись, що всі батьківські вузли завжди більше, ніж дочірні вузли. Як було зазначено у висновку під куповим відсортованим масивом, зображувальне зображення буде таким:
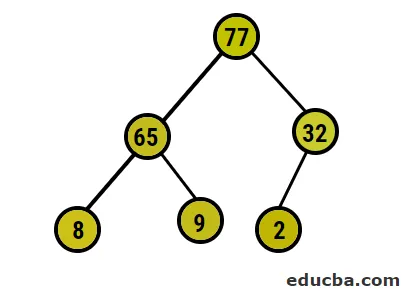
- Після цього ми будемо поміняти кореневий вузол крайнім листовим вузлом, а потім видалити його з дерева. Листовий вузол буде корінцем зараз і знову той самий процес е, щоб знову отримати найвищий елемент у корені
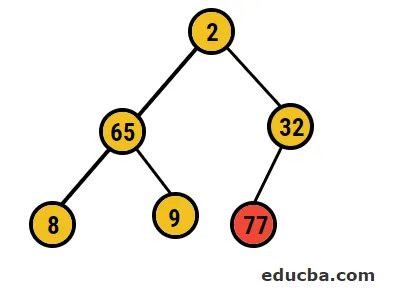
- Отже, у цьому випадку з цього дерева видаляється 77 цифр і поміщається в наш відсортований масив, і процес повторюється.
Вище сказане ми бачили для формування максимуму масиву купи. Цей же процес розглядається і з утворенням масиву міні-купи. Як обговорювалося вище, різниця полягає лише у взаємозв'язку батьківських та дочірніх елементів вузла.
Як вправу ви можете спробувати сформувати сорти купи у порядку зменшення?
Висновок
Хоча існує багато методів сортування, сортування купи вважається однією з кращих методів сортування завдяки своїй часовій та просторовій складності. Складність часу для всіх найкращих, середніх і найгірших випадків становить O (nlogn), де найгірша складність краща, ніж найгірша складність Quicksort, а просторова складність - O (1).
Рекомендовані статті
Це посібник по сортуванню купи в C. Тут ми обговорюємо логіку та кроки для сортування купи з кодом зразка та виводимо разом із зображеннями. Ви також можете переглянути наступні статті, щоб дізнатися більше -
- Сортування купи в Java
- Сортування вибору в Java
- Паліндром у програмі С
- Шаблони в програмуванні на С
- Сортування купи в C ++ (Алгоритм)
- Сортування купи в Python
- C Матричне множення програмування