
Функція Excel SIN (Зміст)
- Функція SIN в Excel
- Як використовувати функцію SIN в Excel?
Функція SIN в Excel
Вміння обчислити не охоплює всієї математики. Це її підрозділ, хоч і життєво важливий при його застосуванні. За минулі роки це було обмежуючим фактором, за винятком знаменитих та надзвичайно талановитих «людських калькуляторів», таких як Шакунтала Деві. Але комп’ютери тепер дозволяють зробити всю математику більш інтелектуальною. Поняття та теореми математики зараз більш помітні, ніж будь-коли раніше.
Excel дуже вміло обробляє безліч математичних моделей, озброєний великою сукупністю математичних та логічних функцій для підтримки різних операцій. Він надає цілий набір тригонометричних функцій, щоб допомогти нам, коли ми вирушаємо у світ тригонометрії.
Отже, для вирішення тригонометричної функції Sine вона забезпечує функцію SIN . Це основна тригонометрична функція, але це стане в нагоді особливо, якщо ви працюєте у виробництві, навігації та комунікаціях. Але важливо відзначити, що Excel використовує радіани, а не градуси для обчислення будь-якого тригонометричного виразу. Існує два способи цього:
- Нагадаємо, що π = 180 °. Отже, якщо кут у градусах, помножте його на π / 180 °, щоб перетворити його на радіани. У Excel це перетворення можна записати PI () / 180. Наприклад, для перетворення 60 ° в радіани, вираз Excel буде 60 * PI () / 180, що дорівнює 1, 0472 радіану.
- Excel також оснащений дуже корисним інструментом, який зазвичай називають RADIANS. Він приймає кут як аргумент, в якому кут посилається на градуси, які необхідно перетворити на радіани. Візьмемо приклад, коли вираз, який використовується для перетворення 210 ° в радіани, є "RADIANS (210)", і він оцінює до 66519 радіанів.
І навпаки, утиліта DEGREES не менш важлива. Ця функція може бути використана для прямо протилежної функції RADIANS шляхом перетворення радіанів у градуси. Наприклад, DEGREES (PI () / 2) оцінює 90.
Як використовувати функцію SIN в Excel?
Давайте розберемося, як використовувати функцію SIN в Excel, використовуючи кілька прикладів та реальних ілюстрацій функції SIN у Excel.
Ви можете завантажити цей шаблон шаблону Excel з функцією SIN тут - Шаблон Excel Excel ШаблонФункція SIN в Excel - приклад №1
Обчислення значення синуса за допомогою функції SIN в Excel
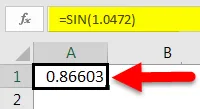
Щоб знайти синус певного числа, треба спочатку записати = SIN () у певну комірку.

Як видно з наведеного вище скріншоту, функція SIN в Excel очікує число як вхід. Це число зазвичай представляє значення в радіанах.
Тож у цьому випадку ми напишемо “= SIN (1.0472)”, де 1, 0472 - радіани, еквівалентні 60 градусам.
Як тільки ми це зробимо, ми отримаємо значення SIN 60 градусів.
Функція SIN в Excel - приклад №2
Обчислення значення синуса за допомогою функції SIN та RADIAN в Excel
Тепер давайте подивимось, як ми можемо використовувати SIN більш продуктивним способом, якщо ми не знаємо точне значення радіану на ступінь.
Ми будемо використовувати RADIANS () для з'ясування значення радіану, яке ми передамо як аргумент функції SIN.
Отже, ми почнемо з попередньої версії SIN ():

Далі ми передамо RADIANS (60) як аргумент функції SIN, де 60 - значення у градусах.

Як ми бачимо з наведеного вище прикладу, RADIANS () приймає значення в градусах. Отже, ми передамо 60 як значення RADIANS ().

Потім натисніть Enter. Це дає наступний результат.

Отже, ми бачимо, що результат такий самий, як перший приклад.
Функція SIN в Excel - приклад №3
Розрахунок значення синуса за допомогою функції SIN та PI в Excel
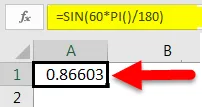
Існує ще один спосіб перетворення значення градуса в радіани для нашого використання у функції SIN. З нашого часу в школі ми пам’ятаємо, що π = 180 °. Отже, якщо кут у градусах, помножте його на π / 180 °, щоб перетворити його на радіани. У Excel це перетворення можна записати PI () / 180. Наприклад, для перетворення 60 ° в радіани, вираз Excel буде 60 * PI () / 180, що дорівнює 1, 0472 радіану.
Подивимося, як це працює:
Почнемо з написання функції SIN так само, як вище.

Далі ми безпосередньо передамо 60 ° як аргумент функції SIN. Але це не дасть нам відповідного значення в радіанах 60 градусів. Отже, ми помножимо 60 на PI () / 180.

Це дасть нам такий результат:
Як ми бачимо, це те саме, що наведені вище приклади.
Функція SIN в Excel - приклад №4
Тепер розглянемо ще один приклад, який показує результати функції SIN для різних значень.

Пояснення результатів, показаних у наведеній вище таблиці:
Випадок 1 і 2:
3.14 - це значення Pi, і ми можемо використовувати обидва методи, щоб отримати значення 0. Це в основному означає, що SIN з Pi radian дорівнює 0 .
Випадок 3 та 4:
Radians і Pi / 180 мають однакове значення в математиці, отже, функція SIN дає однакове значення. Обидва приклади мають на увазі SIN 30 градусів, що дає значення 0, 5.
Випадок 5 і 6:
SIN 45 = 0, 85 - це SIN з 45 радіанів, що означає, що за замовчуванням excel приймає всі кути в радіанах, а не ступінь. Щоб перетворити його в ступінь, ми можемо використовувати радіанову функцію і отримати SIN 45 градусів, як показано в останньому рядку. тобто SIN (RADIANS (45)) = 0.707 або 0.71
Функція SIN в Excel - приклад №5
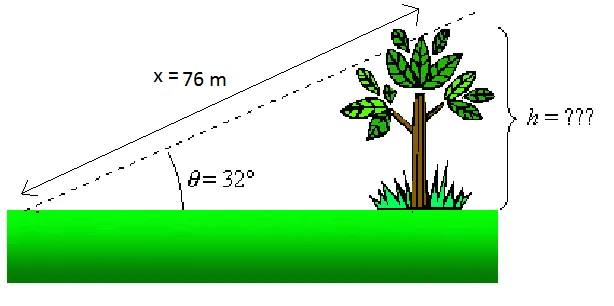
Скажімо, наприклад, ми хочемо знати висоту дерева на малюнку, показаному вище. Ми знаємо, що якщо ми стоїмо на відстані 76 м від вершини дерева (х = 76 м), то лінія огляду до вершини дерева дорівнює 32 ° щодо горизонту (θ = 32 °). Ми знаємо, що:
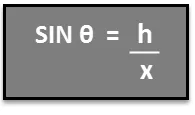
Отже, щоб вирішити висоту дерева h, знаходимо h = x SIN θ.

Функція SIN має лише один аргумент, який є числом. Для його обчислення потрібне число. Тому важливо перетворити градуси в число в радіанах, перш ніж знайти його синус.
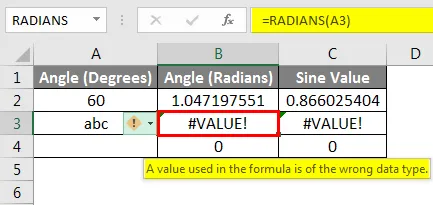
Функція SIN відображає # VALUE! помилка, якщо посилання, яке використовується як аргумент функції, вказує на комірку, що містить текстові дані. У наведеному нижче прикладі посилання на комірку третього ряду вказує на текстову мітку в куті (градуси) . Оскільки функції SIN підтримують лише число в якості аргументу, SIN оцінить на помилку, в цьому випадку #VALUE! . Якщо комірка вказує на порожню комірку, функція повертає значення нуля, як показано в прикладі нижче. Тригонометричні функції Excel інтерпретують порожні комірки як нуль, а синус нульових радіанів дорівнює нулю.
Функція SIN в Excel - приклад №6
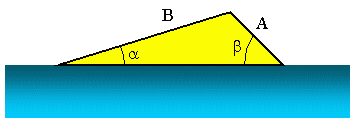
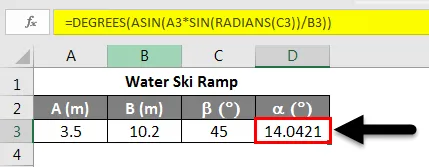
Тепер, припустимо, ми хочемо з'ясувати кут запуску пандуса для водних лиж, як на малюнку вище. Відомо, що А = 3, 5 м, В = 10, 2 м і b = 45, 0 °. Тепер, щоб знайти a, ми можемо використовувати Закон синусів. У цьому сценарії його можна записати так:
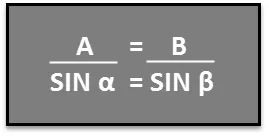
Ми можемо переорганізувати це рівняння у такий спосіб:
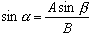
Використовуючи дугу дуги або зворотну силу, ми можемо з’ясувати кут α . Застосовуючи рівняння, показане нижче.

Приклад №7
У нашому заключному тригонометричному прикладі ми будемо використовувати Excel для вивчення тригонометричної ідентичності:
sin²θ + cos²θ = 1
Зауважте, що на скріншоті нижче ця ідентичність справедлива, коли θ задається і в радіанах, і в градусах.

Зверніть увагу, що опис одиниці кута θ розміщується в інших осередках, ніж числа. Якщо ми помістимо числа і одиниці в одну клітинку, Excel не зможе диференціювати число від тексту, і тому ми не зможемо посилатись на комірки для використання в рівнянні, і це призведе до # VALUE! помилка.
Що потрібно пам’ятати
- Майте на увазі, що функція SIN у excel працює з Radian за замовчуванням.
- Перетворіть число, як потрібно в Radian або Degree, використовуючи функцію RADIANS або DEGREES.
- Ви можете використовувати функцію PI () для отримання точних результатів функції SIN під час роботи з π.
Рекомендовані статті
Це було керівництвом щодо функції SIN в Excel. Тут ми обговорили, як використовувати функцію SIN в Excel разом з практичними прикладами та шаблоном Excel, який можна завантажити. Ви також можете ознайомитися з іншими запропонованими нами статтями -
- Важливі функції математики в Excel (легко)
- Посібник з розподілу формул в Excel
- Важливі розширені формули та функції Excel
- Чит-лист формул Excel