Зразок стандартної формули відхилення

Зразок стандартної формули відхилення (зміст)

Формула
Приклади

У статистиці стандартне відхилення в основному є мірою для знаходження дисперсії значень набору даних від середнього значення набору даних. Він вимірює відстань цієї точки даних та середнє значення. Так що вище стандартне відхилення, тим вище буде дисперсія, і точки даних, як правило, далекі від середнього. Аналогічно, нижнє стандартне відхилення означає, що точки даних будуть ближче до середнього. Це дуже корисно для порівняння наборів даних, які можуть мати однакове середнє значення, але різний діапазон.

Зазвичай, обчислюють стандартне відхилення даних про населення, але іноді дані про населення настільки величезні, що неможливо знайти стандартне відхилення для цього. У цьому випадку обчислюється вибіркове стандартне відхилення, яке стане представником стандартного відхилення популяції. Тож ми будемо вважати, що вибірка є правильним представленням сукупності та будемо зосереджуватися на стандартному відхиленні вибірки в цій статті.

Припустимо, у вас є набір даних X з точками даних (X1, X2 …… ..Xn).

Формула стандартного відхилення популяції задається:

Population Standard Deviation = √ (Σ (X _i – X _m ) ² / n )

Якщо вам не надано всю сукупність і маєте лише вибірку (скажімо, X - вибіркова сукупність даних сукупності), то формула стандартного відхилення вибірки задається:

Sample Standard Deviation = √ (Σ (X _i – X _m ) ² / (n – 1))

Де:

X _i - i- ^е значення набору даних
X _m - середнє значення набору даних
n - Загальна кількість точок даних

Спочатку формула може виглядати заплутаною, але над цим реально працювати. Нижче наведено етапи, за якими можна обчислити стандартне відхилення вибірки:

Знайдіть кількість точок у наборі даних, тобто n
Тоді наступним кроком є пошук середнього значення вибірки. Це в основному середнє значення всіх значень.
Після цього для кожної точки даних знайдіть відмінність цього значення від середнього значення, а потім покладіть його на квадрат.
Візьміть суму всіх значень на вищевказаному кроці та розділіть їх на n-1.
Останній крок - взяти квадратний корінь числа, обчисленого вище.

Існує ще один спосіб розрахунку сукупності та стандартного відхилення просто за допомогою функції STDEV.P () для стандартного відхилення популяції та функції STDEV.S () для стандартного відхилення вибірки в excel.

Приклади зразкової стандартної формули відхилення (із шаблоном Excel)

Візьмемо приклад, щоб краще зрозуміти розрахунок вибіркового стандартного відхилення.

Ви можете завантажити цей зразок стандартного шаблону формули Excel Formula Excel тут - Зразок стандартного шаблону формули Excel Excel

Зразок стандартної формули відхилення - приклад №1

Скажімо, у нас є два вибіркові набори даних A&B і кожен містить 20 випадкових точок даних і мають однакове середнє значення. Обчисліть вибіркове стандартне відхилення для набору даних A&B

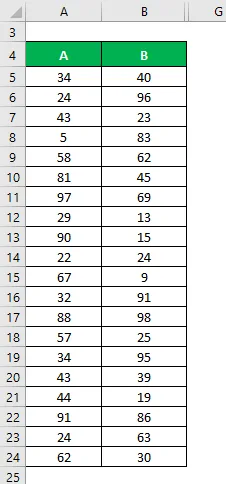
Рішення:

Середнє значення обчислюється як:

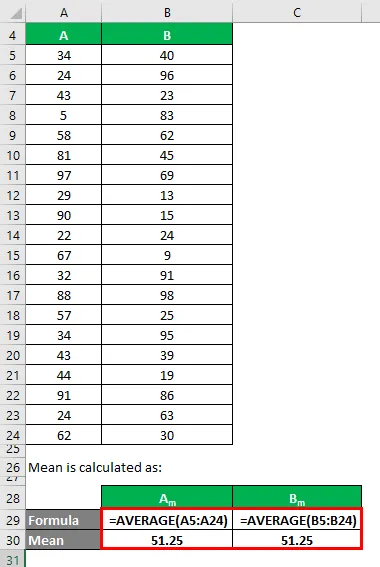
Середнє значення набору даних A = 51, 25
Середнє значення набору даних B = 51, 25

Тепер нам потрібно обчислити різницю між точками даних та середнім значенням.

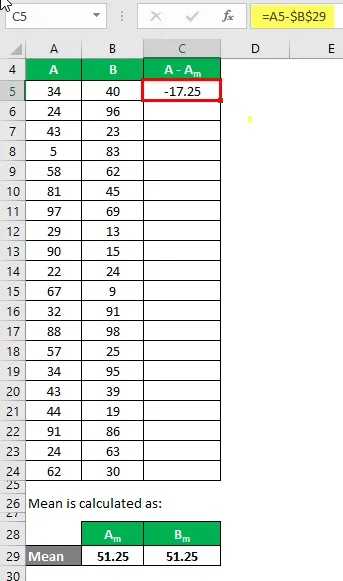
Аналогічно обчисліть для всіх наборів даних А.

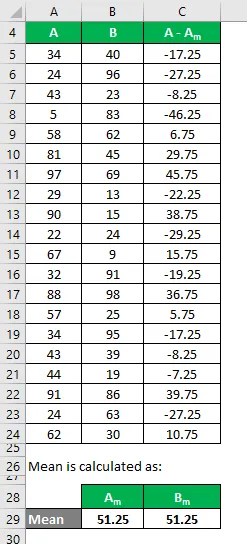
Аналогічно обчисліть його і для набору даних B.

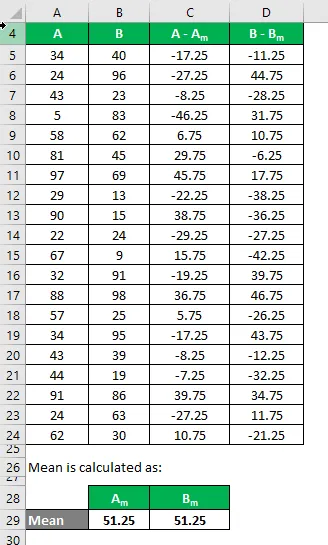
Обчисліть квадрат різниці для обох наборів даних A і B.

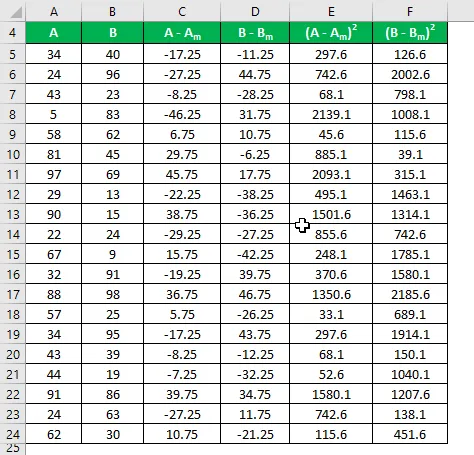
Стандартне відхилення вибірки розраховується за формулою, наведеною нижче

Зразок стандартного відхилення = √ (Σ (X _i - X _m ) ² / (n - 1))

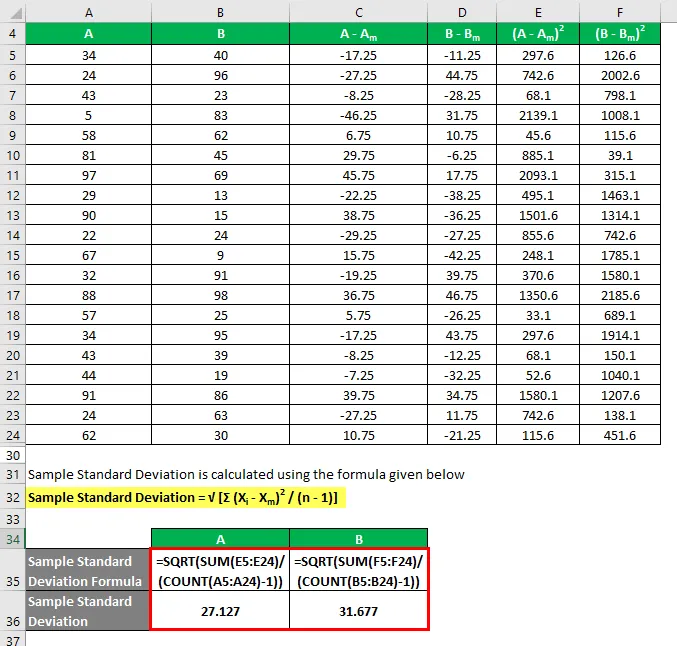
Отже, якщо ви бачите тут, хоча обидва набори даних мають однакове середнє значення, B має більш стандартне відхилення, ніж A, що означає, що точки даних B є більш розсіяними, ніж A.

Зразок стандартної формули відхилення - приклад №2

Скажімо, ви дуже ризикований інвестор і хочете вкласти гроші на фондовому ринку. Оскільки апетит до ризику низький, ви хочете інвестувати в безпечні акції, які мають нижче стандартне відхилення. Ваш фінансовий радник запропонував вам 4 акції, з яких ви можете вибрати. Ви хочете вибрати 2 акції серед цих 4, і ви вирішите це на основі нижчого стандартного відхилення.

Ви отримали інформацію про їх історичну віддачу за останні 15 років.

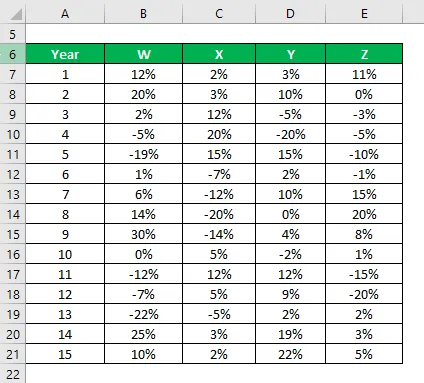
Рішення:

Зразок стандартного відхилення розраховується за формулою excel

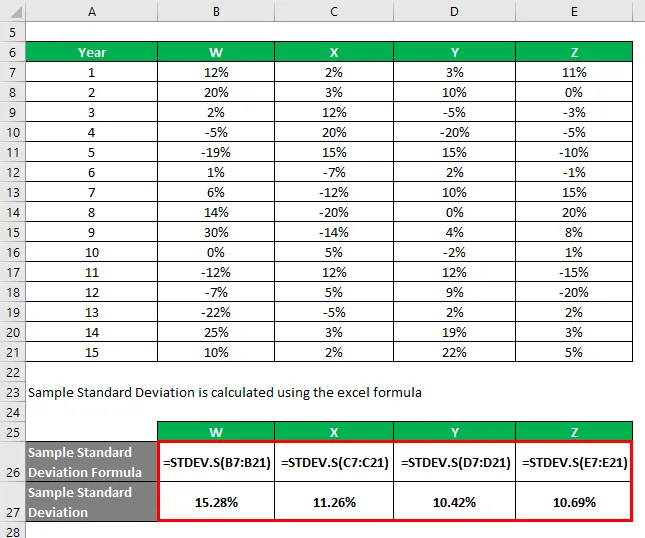
На основі інформації та типового відхилення вибірки ви виберете акції Y та Z для інвестування, оскільки вони мають найменше стандартне відхилення.

Пояснення

Ми обговорюємо значення стандартного відхилення від статистичної точки зору, але воно також відіграє важливу роль, якщо говорити про фінансову точку зору. У фінансах це, в основному, міра ризику, яку несе інвестиція, і наскільки ризикована ця інвестиція. Виходячи з ризику, який має інвестиція, інвестори можуть потім розрахувати мінімальну віддачу, необхідну для компенсації цього ризику. Як і у вищенаведеному прикладі, оскільки Y і Z мають менший стандартний відхилення, це означає, що менша мінливість у поверненні цих запасів, тому вони менш ризиковані. Один момент, використовуючи інструмент стандартного відхилення, ми маємо пам’ятати, що на нього сильно впливають екстремальні значення або переживаючі. Ці атрибути можуть перекосити значення стандартного відхилення.

Актуальність та використання зразка стандартної формули відхилення

Стандартне відхилення допомагає інвесторам та аналітикам знайти коефіцієнт ризику та винагороди або коефіцієнт Шарпа для інвестиції. В основному, кожен може заробити безризикову норму прибутку, інвестуючи в казначейство та безризикові цінні папери. Але повернення вище і вище - це надлишковий прибуток, і для досягнення цього рівня ризику, який потрібно взяти, є мірою коефіцієнта Шарпа:

Коефіцієнт різкості = (рентабельність інвестицій - Безризикова ставка) / Стандартне відхилення

Отже, чим вище коефіцієнт Шарпа, тим краще інвестиції.

Як ми говорили, що стандартне відхилення є мірою ризику, однак нижче значення стандартного відхилення не завжди є переважним. Якщо інвестор має більш високий апетит до ризику і хоче інвестувати більш агресивно, він буде готовий ризикувати і вважатиме за краще відносно більш високе стандартне відхилення, ніж інвестор, який не ризикує. Отже, все залежить від того, який рівень ризику готовий взяти інвестор.