✅ Формула розподілу Пуассона - Калькулятор (приклади з шаблоном Excel)

Що таке формула розподілу Пуассона?

Формула розподілу Пуассона (Зміст)

Формула
Приклади
Калькулятор

Що таке формула розподілу Пуассона?

У вірогідності та статистиці існує три типи розподілів на основі безперервних та дискретних даних - нормальні, двочленні та пуассонові розподіли. Нормальний розподіл часто є кривою дзвона. Поширення Пуассона часто називають Поширенням рідкісних подій. Це в основному використовується для прогнозування ймовірності подій, які відбудуться, виходячи з того, як часто подія траплялася в минулому. Це дає можливість заданої кількості подій, що відбуваються за певний період. Він використовується у багатьох ситуаціях із реального життя.

Формула для пошуку розподілу Пуассона наведена нижче:

P(x) = (e ^-λ * λ ^x) / x!

Для х = 0, 1, 2, 3…

Цей експеримент, як правило, підраховує кількість подій, що відбулися в районі, відстані чи обсягу. Поряд з цим, можна знайти Ланцюг подій, що є не що інше, як ланцюг виникнення тієї ж події протягом певного періоду часу. Розподіл Пуассона має такі загальні характеристики.

Подія може статися в будь-який час у будь-який час.
Подія може враховувати будь-які заходи, такі як обсяг, площа, відстань та час.
Однак ймовірність того, що подія відбудеться в будь-яких зазначених вище заходах, однакова.
Кожна подія не залежить від усіх інших подій, що означає, що ймовірність того, що подія не відбудеться, не впливає на інші події, що відбуваються одночасно.

Приклади формули розподілу Пуассона

Візьмемо приклад, щоб краще зрозуміти розрахунок розподілу Пуассона.

Ви можете завантажити цей шаблон формули Excel-формули розповсюдження Пуассона тут - Шаблон формули Excel-формули розподілу Пуассона

Формула розподілу Пуассона - приклад №1

Середня кількість щорічних аварій, що трапляються на платформі залізничного вокзалу під час руху поїздів, становить 7. Для визначення ймовірності того, що в цьому році на одній платформі на цій же платформі трапляється рівно 4 випадки, можна використовувати формулу розподілу Пуассона.

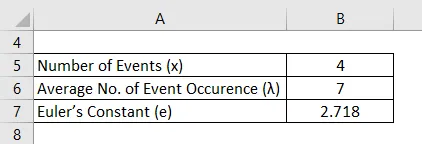
Рішення:

Розподіл Пуассона розраховується за формулою, наведеною нижче

P (x) = (e ^-λ * λ ^x) / x!

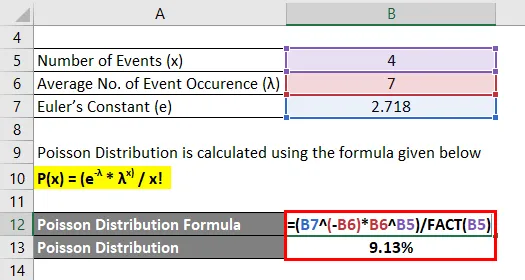
P (4) = (2.718 ^-7 * 7 ⁴⁾ / 4!
P (4) = 9, 13%

Для наведеного прикладу є 9, 13% шансів, що трапиться точно така ж кількість ДТП, яка може статися цього року.

Формула розподілу Пуассона - приклад №2

Кількість помилок друку, допущених машиністкою, має розповсюдження Пуассона. Помилки робляться самостійно із середньою швидкістю 2 на сторінці. Знайдіть ймовірність того, що тристорінковий лист не містить помилок.

Тут середній показник на сторінку = 2 і середній показник на 3 сторінки (λ) = 6

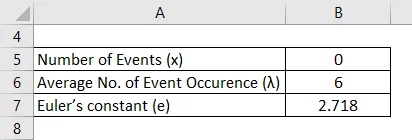
Рішення:

Розподіл Пуассона розраховується за формулою, наведеною нижче

P (x) = (e ^-λ * λ ^x) / x!

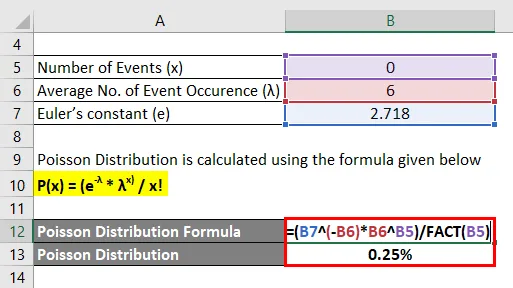
P (0) = (2.718 ^-6 * 6 ⁰ ) / 0!
P (0) = 0, 25%

Отже, є 0, 25% шансів, що не буде помилок на 3 сторінках.

Примітка : x ^{0 =} 1 (будь-яке значення 0 завжди буде 1) ; 0! = 1 (нульовий показник завжди буде 1)

Пояснення

Нижче подано покроковий підхід до обчислення формули розподілу Пуассона.

Крок 1: е - константа Ейлера, яка є математичною постійною. Як правило, значення e 2, 718 .

Крок 2: X - кількість фактично відбулися подій. Він може мати такі значення, як наступні. х = 0, 1, 2, 3…

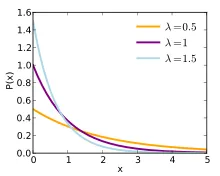
Крок 3: λ - середня (середня) кількість подій (також відома як "Параметр розподілу Пуассона"). Якщо взяти простий приклад для обчислення λ => 1, 2, 3, 4, 5. Якщо ви застосовуєте той самий набір даних у наведеній вище формулі, n = 5, отже, середнє = (1 + 2 + 3 + 4 + 5) / 5 = 3. Для великої кількості даних знайти медіану вручну неможливо. Тому важливо використовувати формулу для великої кількості наборів даних. Тут, обчислюючи розподіл Пуассона, ми зазвичай отримуємо середнє число безпосередньо. Виходячи зі значення λ, графік Пуассона може бути одномодальним або бімодальним, як показано нижче.

Крок 4: х! є Фактор фактичних подій, що відбулися х. Нижче наведено приклад того, як обчислити факторіал для заданого числа.

Якщо ви берете простий приклад для обчислення Факторалів реального набору даних => 1, 2, 3, 4, 5.

х! = x * (x-1) * (x-2) * (x-3) * …… 3 * 2 * 1
5! = 5 * (5-1) * (5-2) * (5-3) * (5-4)
5! = 5 * 4 * 3 * 2 * 1
5! = 120

Актуальність та використання формули розподілу Пуассона

Розподіл Пуассона може працювати, якщо набір даних - це дискретний розподіл, кожне подія незалежно від інших подій, що відбулися, описує дискретні події протягом інтервалу, події в кожному інтервалі можуть становити від нуля до нескінченності і означають, що кількість подій повинна бути постійний протягом усього процесу. Залежно від значення параметра (λ), розподіл може бути одномодальним або бімодальним. Розподіл Пуассона - це дискретний розподіл, означає, що подію можна констатувати лише як відбувається чи не так, що відбувається, тобто число може бути вказане лише цілими числами. Дробові явища події не є частиною цієї моделі. Результати результатів можна класифікувати як успіх чи невдачу. Це широко використовується у світі:

Аналітика даних для прогнозного аналізу даних
Прогнози фондового ринку
Прогнози ринку збуту
Прогнози ланцюга попиту та пропозиції
Легко доступний на платформах Amazon Web Services (AWS)
Огляд та оцінка покриття страхування бізнесу

Інші програми розповсюдження Пуассона - це більш відкриті проблеми. Наприклад, він може бути використаний для визначення мінімальної кількості ресурсів, необхідної в колл-центрі, виходячи із середнього кількості отриманих дзвінків та викликів на утриманні. Коротше кажучи, список додатків можна додавати все більше і більше, оскільки він використовується у всьому світі практичною статистичною метою.

Калькулятор формули розподілу Пуассона

Можна скористатися наступним калькулятором Пуассона розподілу

λ
х
P (x)

P (x) =	(e- ^λ * λ ^x ) / x!
	(0 ^-0 * 0 ⁰ ) / 0! =	0

Формула розподілу Пуассона в Excel (із шаблоном Excel)

Тут ми зробимо ще один приклад розподілу Пуассона в Excel. Це дуже легко і просто.

Обчисліть розподіл Пуассона в Excel за допомогою функції POISSON.DIST.

Нижче наведено синтаксис формули розподілу Пуассона в Excel.

Розподіл Пуассона має такий аргумент:

Де,

x = кількість подій, для яких потрібно знати ймовірність.
Середня = Середня кількість випадків за період часу.
Кумулятивна = Його значення буде Неправильним, якщо нам потрібен точний випадок події, і Істинним, якщо кількість випадкових подій буде між 0 і цією подією.

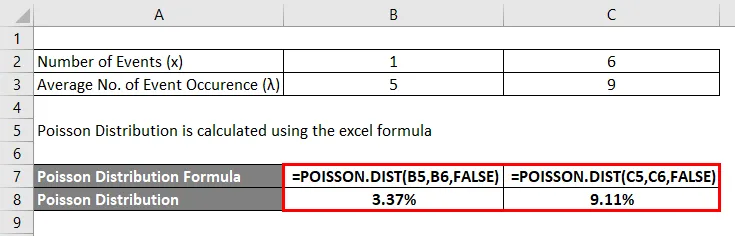
Розподіл Пуассона розраховується за формулою excel

Формула розподілу Пуассона - Калькулятор (приклади з шаблоном Excel)