
Вступ до математичних функцій на С
У цій статті перераховані різні математичні функції, які використовуються в мовах програмування на С із ілюстрацією робочого коду. Комп'ютери роблять величезні математичні обчислення та аналізи величезних чисел, для цього ми використовували математичні функції в C. Перш ніж почати з, нам потрібно знати, що на мовах C використовується заголовок / бібліотека під назвою Math.h для різних математичних функцій. Це допомагає в обчисленні тригонометричних операцій, логарифмів, абсолютних значень, квадратних коренів. Отже, давайте вивчимо різні типи функцій, які використовуються в цій бібліотеці. Всі ці функції приймають подвійне значення типу даних і повертають те саме.
Різні математичні функції в С
Давайте побачимо різні функції, визначені в math.h, і бібліотека Math класифікується на три основні типи: тригонометричні функції, математичні функції, функції журналу / виставки. Для реалізації наведених нижче функцій обов'язково потрібно включити або в код.
1. поверх (подвійний а)
Ця функція повертає найбільше ціле значення, яке не перевищує значення "a". Він округляє значення і в результаті повертає подвійне. Для негативних чисел він поводиться по-різному, оскільки вони округляються до наступного від’ємного числа.
Наприклад: підлога (7.2) - 7, 0
поверх (-7, 2) становить -8, 0
Приклад:
Ця програма ілюструє, як обчислити підлогу для оголошеного значення та округлює наступне значення 10.
#include
#include
int main()
(
double f= -9.33;
int final;
final = floor(f);
printf("Floor value of %.2f = %d", f, final);
return 0;
)
Вихід:

2. стеля ()
Синтаксис:
double ceil (double b)
Ця функція повертає найменше ціле значення, яке більше або дорівнює b, і округляє значення вгору. Для від’ємного значення воно рухається вліво. Приклад 3.4 повернення -3 має вихід.
Приклад:
Ця програма пояснює, приймаючи вхід у аргумент float і повертає значення ceil.
#include
#include
int main()
(
float n, ceilVal;
printf(" Enter any Numeric element : ");
scanf("%f", &n);
ceilVal = ceil(n);
printf("\n The Value of %.2f = %.4f ", n, ceilVal);
return 0;
)
Вихід:

3. Sqrt ()
Ця функція повертає квадратний корінь заданого числа.
Синтаксис:
sqrt( arg)
Приклад:
Нижче наведений код пояснює найвідомішу математичну функцію sqrt (), беручи значення 'n' для обчислення квадратного кореня для різних значень 'n'.
#include
#include
int main()
(
double n, output;
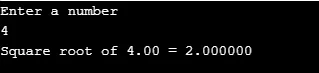
printf("Enter a number\n");
scanf("%lf", &n);
output = sqrt(n);
printf("Square root of %.2lf = %f", n, output);
return 0;
Вихід:
4. круглий ()
Ця функція округляє найближче значення заданого входу. Це викидає помилку, якщо значення занадто велике. Інші функції, такі як lround (), llround (), також округляють найближче ціле число.
Синтаксис:
int round(arg)
Приклад:
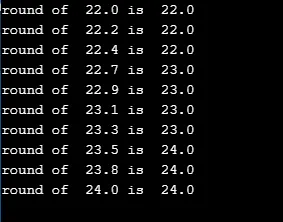
Наведений нижче код дуже простий, що дозволяє округлювати до найближчого значення 'r' у циклі for.
#include
#include
int main ()
(
for(double r=110;r<=120;r+=1.1)
printf("round of %.1lf is %.1lf\n", r/5.0, round(r/5.0));
return 0;)
Вихід:
5.pow ()
Ця функція повертає живлення для заданого числа (a b ). Він повертає підняту до сили b, яка має два параметри бази та показника.
Приклад:
У нижньому вихідному коді ми дозволяємо користувачеві вводити вхідне значення для обчислення потужності заданих двох аргументів.
#include
#include
int main()
(
int r, ba, expr;
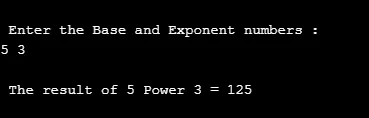
printf("\n Enter the Base and Exponent numbers : \n");
scanf("%d %d", &ba, &expr);
r = pow(ba, expr);
printf("\n The result of %d Power %d = %d ", ba, expr, r);
return 0;
)
вихід:
6. ствол ()
Ця функція допомагає обрізати задане значення. Він повертає цілі значення. Для урізання плаваючих та подвійних значень використовуються truncf (), truncl ().
Синтаксис:
double trunc(a);
Приклад:
Нижче вихідного коду знаходяться два вхідні значення a, b для урізання подвійних значень.
#include
#include
void main() (
double m, n, a, b;
a = 56.16;
b = 85.74;
m = trunc(a);
n = trunc(b);
printf("The value of a: %lf\n", m);
printf("The value of a: %lf\n", n);
)
Вихід:

7. fmod ()
Ця функція повертає залишок для заданих двох вхідних значень, коли m ділиться на n.
Синтаксис:
double fmod(double I, double j)
Приклад:
У наведеному нижче прикладі потрібно два значення від користувача, щоб обчислити залишок за допомогою функції fmod ().
#include
#include
int main()(
double fiN;
double secN;
double n;
printf("Enter the first number : ");
scanf("%lf", &fiN);
printf("Enter the second number : ");
scanf("%lf", &secN);
printf("fmod(firstNumber, secondNumber) is %lf \n", fmod(fiN, secN));
)
Вихід:

Тригонометричні функції
Нижче наведено різні функції тригонометричних:
1. гріх ()
Ця вбудована функція дає синусове значення заданого числа, обчислює значення з плаваючою комою. asin () обчислює дугу, для гіперболічних - це sinh ().
Синтаксис:
return type sin(y);
y повертає значення в радіанах, а тип повернення - подвійний.
Приклад:
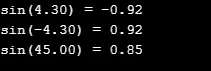
У наступному вихідному коді я взяв два різних вхідних значення для обчислення значення sin та повертає подвійне.
#include
#include
int main()
(
double a;
double z;
a = 4.3;
z = sin(a);
printf("sin(%.2lf) = %.2lf\n", a, z);
a = -4.3;
z = sin(a);
printf("sin(%.2lf) = %.2lf\n", a, z);
a = 45;
z = sin(a);
printf("sin(%.2lf) = %.2lf\n", a, z);
return 0;
)
Вихід:
2. sinh ()
Ця математична функція обчислює значення тригонометричного дотичного синуса для заданого числа.
Синтаксис:
double sinh(x);
Приклад
У наведеному нижче вихідному коді синусовий гіперболічний обчислюється шляхом оголошення вхідного значення.
#include
#include
#define PI 3.141592654
int main()
(
double gt = 3.60, z;
z = sinh(gt);
printf("Sine hyperbolic of %.2lf is = %.2lf", gt, z);
return 0;
)
Вихід

3. cos ()
Ця математична функція визначає тригонометричне значення косинусу для даного елемента.
Синтаксис: return type cos(argument);
#include
#include
#define PI 3.14
int main()
(
double cVal, rVal, dVal;
for(int i=0;i<=2;i++)
(
printf(" Enter an Angle in degrees : ");
scanf("%lf", &dVal);
rVal = dVal * (PI/180);
cVal = cos(rVal);
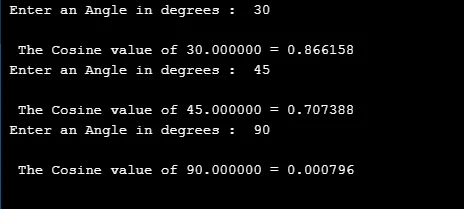
printf("\n The Cosine value of %f = %f ", dVal, cVal);
printf("\n");
)
return 0;
)
Вихід:
4. cosh ()
Він повертає гіберболічний косинус за задане значення.
Синтаксис:
double cosh(y);
Приклад
Наведений нижче приклад показує, що для обчислення гіперболічних значень потрібно два різних вхідних значення.
#include
#include
int main ()
(
double k, r;
k = 0.6;
r = cosh(k);
printf("Hyperbolic cosine of %lf is = %lf\n", k, r);
k = -0.8;
r = cosh(k);
printf("Hyperbolic cosine of %lf is = %lf\n", k, r);
return 0;)
Вихід

5. засмага ()
Ця математична функція бібліотеки обчислює дотичні значення кута для математичного виразу і вимірюється в радіанах.
Його можна оголосити як
double tan(arguments);
Приклад
У наступному вихідному коді значення засмаги обчислюється для наступних кутів, які збільшуються за допомогою циклу.
# include
# include
# include
void main()
(
float z ;
int k ;
char ch ;
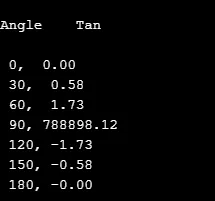
printf("\nAngle \t Tan \n") ;
for (k = 0; k <= 180; k = k + 30)
(
z = k * 3.14159 / 180 ;
printf("\n %d, %5.2f", k, tan(z));
)
getch() ;
)
Вихід:
6. tanh ()
Функція tanh () повертає гіперболічну дотичну даного значення. Він займає один параметр. Крім того, щоб знайти дотичну для довгих подвійних і поплавкових tanhl () і tanhf () використовуються для обчислення.
Синтаксис:
double tanh( val);
Приклад:
Дотична гіберболіка розраховується для значень 'j', використовуючи для циклів. Подивимось, як це працює.
#include
#include
#define PI 3.141592654
int main()
(
double val, r;
for(double j=0.60; j<=2.0;j+=.30)
(
r = tanh(j);
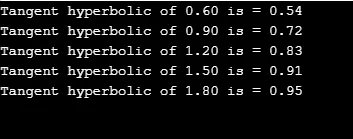
printf("Tangent hyperbolic of %.2lf is = %.2lf", j, r);
printf("\n");
)
return 0;
)
Вихід:
Журнал арифметичних функцій
Нижче наведено різні функції арифметики журналу:
1. exp ()
Ця функція виконує обчислення експоненціалу для заданого значення (e x ). Існують також інші підтипи, такі як frexp (), Idexp (), що повертає мантісу і примножується на силу x.
Синтаксис:
return type exp(value);
Приклад:
Програма приймає у користувача числове значення для обчислення показника для заданого значення і повертає подвійне.
#include
#include
int main()
(
double numb, eVal;
printf(" Enter any Numeric Value : ");
scanf("%lf", &numb);
eVal = exp(numb);
printf("\n Exponential Value of e power %lf = %lf ", numb, eVal);
printf("\n");
return 0;
)
Вихід

2. log ()
Ця функція повертає значення логарифму заданого числа. (до базового електронного журналу e )
Синтаксис:
double log(arg);
Приклад:
У наступному прикладі значення журналу для заданого числа обчислюється за допомогою функції. Визначена користувачем функція lgm () робить обчислення і функція викликається в головній функції.
#include
#include
float lgm ( float iv );
int main ()
(
float q, r ;
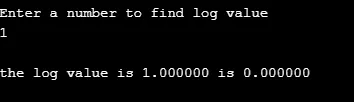
printf ( "\nEnter a number to find log value \n");
scanf ( "%f", &q ) ;
r = lgm ( q ) ;
printf ( "\nthe log value is %f is %f", q, r );
)
float lgm ( float iv ) // function definition
(
float exe ;
exe = log(iv);
return ( exe ) ;
)
вихід:
Висновок
На закінчення ми побачили різні математичні функції, які використовуються в програмуванні на С, і це прямі бібліотечні функції, які слід використовувати. Програми C використовують ці функції для різних математичних операцій. Для вирішення деяких складних версій обчислень ця вбудована функція приносить користь математично орієнтованій мові програмування для повернення простих значень.
Рекомендовані статті
Це посібник з математичних функцій в C. Тут ми обговорюємо різні математичні функції в C на прикладах. Ви також можете ознайомитися з іншими запропонованими нами статтями -
- PHP математичні функції
- Функції JavaScript математики
- Функції передачі в Matlab
- Функції струнного JavaScript
- Вступ до математичних функцій в Python
- Огляд математичних функцій в C #
- C Матричне множення програмування
- Квадратний корінь в PHP
- Приклади квадратного кореня в JavaScript