Лінійна інтерполяція в Excel - Як використовувати лінійну інтерполяцію в Excel?

Лінійна інтерполяція Excel (Зміст)

Що таке Інтерполяція?
Інтерполяція з функцією прогнозу в Excel
Приклади лінійної інтерполяції в Excel

Що таке Інтерполяція?

У світі математики інтерполяція - це метод створення нових точок даних за допомогою відомих точок даних. Інтерполяція оцінює значення на основі наявних значень даних, які можна відновити.

Наприклад, якщо ми їздимо на велосипеді зі швидкістю 60 км / год, а до конкретного пункту доїхали за 1 годину, а якщо ми їдемо зі швидкістю 45 км / год і дісталися певного пункту за 45 хвилин. Тож скільки часу знадобиться для досягнення пункту призначення, якщо ми їдемо зі швидкістю 30 км / годину.

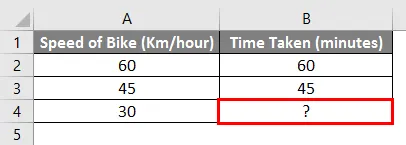
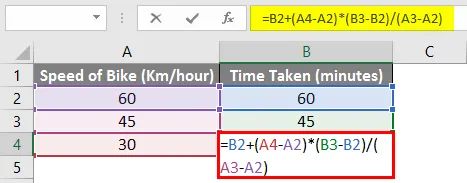
Використовуючи просту математику, ми можемо обчислити відсутні значення у наведеному вище прикладі. Нам потрібно вставити нижченаведену формулу у комірку В4.

= B2 + (A4-A2) * (B3-B2) / (A3-A2)

Тож, виходячи з вищенаведеної формули, ми можемо сказати, що до досягнення пункту призначення потрібно 30 хвилин, якщо ми їдемо зі швидкістю 30 км / годину.

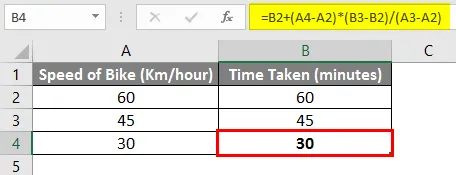
Спробуємо розбити вищевказану формулу та розібратися у формулі докладно.

= B2 + (A4-A2) * (B3-B2) / (A3-A2)

У наведеному вище прикладі останній розділ формули, виділений червоним кольором, обчислює кількість часу, що змінюється, коли швидкість велосипеда змінюється на 1. У нашому прикладі час, який приймається, змінюється на 1 хвилину, коли швидкість велосипеда змінюється на 1 км / годину.

= B2 + (A4-A2) * (B3-B2) / (A3-A2)

Другий розділ (синім кольором вище) обчислює, наскільки далеко наша швидкість велосипеда від першої заданої швидкості велосипеда, а потім помножує його на значення, обчислене вище. Виходячи з нашого прикладу, це 30 (Cell A4) мінус 60 (Cell A2), результат якого множиться на 1 (що дорівнює -30).

= B2 + (A4-A2) * (B3-B2) / (A3-A2)

Нарешті, перший розділ формули (коричневим кольором вище); ми додаємо перше значення швидкості велосипеда. У нашому прикладі це забезпечує кінцевий результат 60 + (-30) * (1) = 30 Хвилини. У школі ми використовували наведену нижче формулу для обчислення відсутнього значення Y.

Y = Y1 + (X-X1) * (Y2-Y1) / (X2 - X1)

Це приклад того, як обчислити пропущені значення за допомогою ручної формули, щоб зрозуміти інтерполяцію.

У Excel є вбудована функція, яка робить аналогічний обчислення, як описано вище, і вона відома як FORECAST Function. Зараз ми детально вивчимо цю функцію.

Інтерполяція з функцією прогнозу в Excel

Прогноз - це функція робочого листа, доступна в MS Excel, і вона використовує лінійну регресію для з'ясування відсутнього значення. Прогноз, як видно з його назви, використовується для прогнозування майбутнього значення точки даних, але також може використовуватися для інтерполяції значення. В основному він використовується для обчислення майбутнього значення на основі існуючих значень конкретного набору даних.

Синтаксис функції прогнозу

Аргументи функції прогнозу:

x - це точка даних, для якої ми хочемо знати отримане значення.
Kknown_y's - Діапазон комірок, що містять значення Y.
Kknown_x - Діапазон комірок, що містять значення X.

Розглянувши той же приклад, спробуємо скористатися функцією прогнозування.

У нашому прикладі

x - Стільниця B4 (як ми хочемо з'ясувати час, відведений при швидкості в 30 км / годину).

K known_y's - Стільниця В2 до Стільниці В3 (Час, що використовується для відомої швидкості велосипеда).

Kknown_x - Стільниця від А2 до Стільця А3 (Швидкість велосипеда, вже задана, на яку ми знаємо витрачений час).

Отже, остаточна формула в комірці B4 буде наведена нижче:

= ПРОГНОЗУВАННЯ (A4, B2: B3, A2: A3)

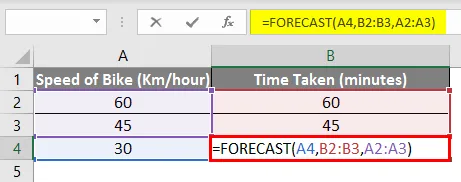
І як ви бачите, кінцевий результат такий самий, тобто 30 хвилин .

Для створення діаграми перейдіть до меню Вставка, клацніть на Розсіювач, а потім виберіть Розсіювач з гладкими лініями та маркерами.

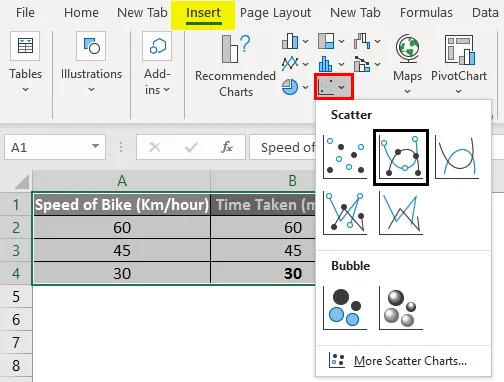
Якщо ми подивимось на нижню діаграму вищенаведеного прикладу, можна сказати, що набір даних має лінійну залежність і відомий як лінійна інтерполяція.

Приклади лінійної інтерполяції в Excel

Розберемо лінійну інтерполяцію в Excel з деякими прикладами.

Ви можете завантажити цей лінійний шаблон інтерполяції Excel тут - Лінійний шаблон інтерполяції Excel

Приклад №1

Припустимо, у вас є дані про продажі та прибуток за попередні роки, і ви хочете знати прибуток поточного року, якщо досягаєте певного рівня продажів.

Подивіться на нижню таблицю. У вас є дані про продажі з 2016 по 2018 рік, і ви хочете знати, яким повинен бути прибуток, якщо ваші продажі становлять Rs. 40, 00 000 у 2019 році.

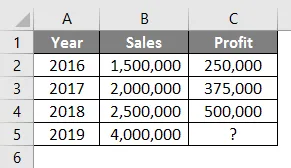
Тож за допомогою функції прогнозування ми можемо інтерполювати прибуток 2019 року, коли продажі становлять Rs. 4 000 000

Формула в комірці С5 буде наведена нижче:

= ПРОГНОЗУВАННЯ (B5, C2: C4, B2: B4)

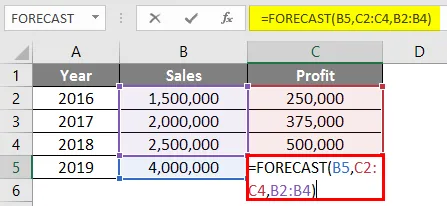
Після використання формули прогнозу відповідь показана нижче.

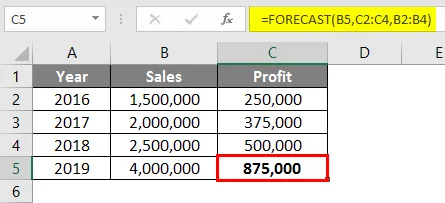
Результатом для функції прогнозування буде Rs. 875 000 на основі даних про продажі та прибуток, наявні з 2016 по 2018 рік.

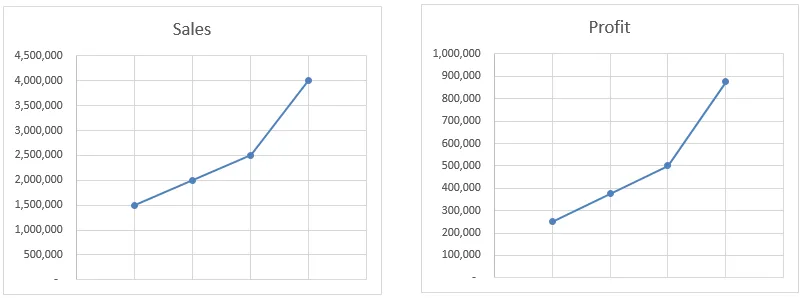
У цьому прикладі функція прогнозування інтерполює значення на основі всіх доступних даних, а не лише початкової та кінцевої точки. Як ви бачите на графіках, прибуток рухається точно так само, як і продажі. Навіть якщо ми обчислимо значення вручну, воно все одно дасть нам той же результат.

Приклад №2

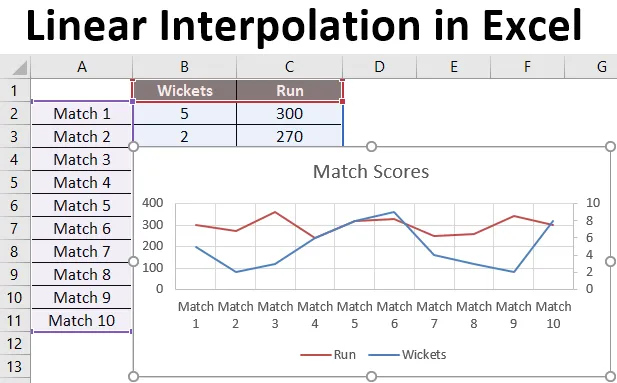
У нас є дані про останні 9 матчів команди з крикету, у яких піклети пройшли і пробігли забиті командою.

Ми хочемо дізнатися, скільки забігів набере команда, якщо випаде 8 хвірт.

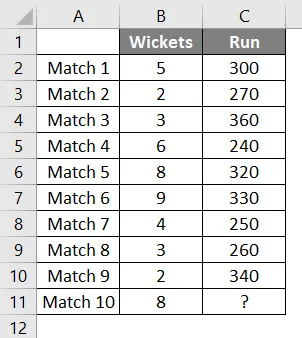
Тому ми знову будемо використовувати ту саму функцію прогнозу, що і вище.

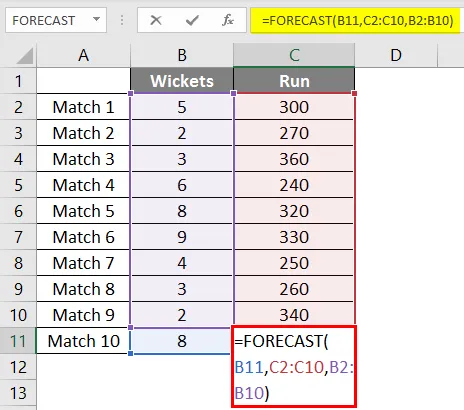
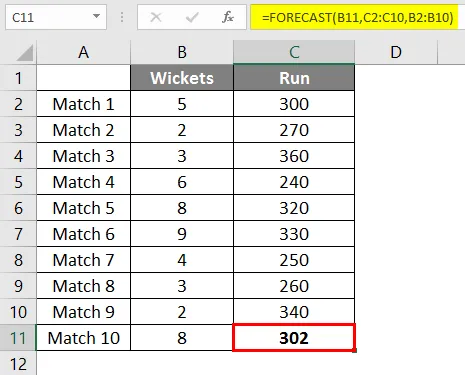
Застосувавши формулу, ми отримуємо результат 302 руна, якщо 8 калиток потрапляють на основі лінійної регресії останніх 9 матчів, які грала команда.

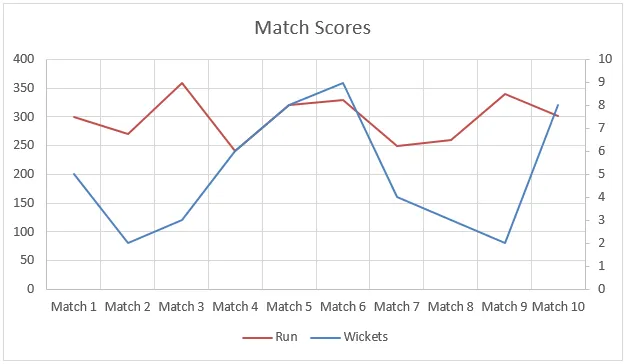
У цьому прикладі дані не були лінійними, і це можна побачити на графіку нижче. Але все-таки функція прогнозування допомогла нам інтерполювати прогони за допомогою даних попередніх матчів.

Що слід пам’ятати про лінійну інтерполяцію в Excel

Функція прогнозу використовується для прогнозування / оцінки значення на основі наявних наявних значень, але це також може допомогти інтерполювати відсутнє значення.
Якщо дані не є лінійними, функція прогнозування не дасть точного значення, яке базується на лінійній інтерполяції, але дасть найближче значення.
Якщо x у функції прогнозу є текстовою чи нечисловою, функція прогнозу повертає помилку #VALUE.
Якщо Kknown_x та Kknown_y не містять даних або містять інший набір точок даних, функція прогнозування призведе до помилки # N / A.
Якщо дисперсія знань_x дорівнює нулю, функція прогнозування дає помилку # DIV / O.