
Вступ до біноміального розподілу в R
У цій статті описано, як використовувати біноміальні розподіли в R для кількох операцій, пов'язаних з розподілом ймовірностей. Бізнес-аналіз використовує біноміальну ймовірність для складної проблеми. R має численні вбудовані функції для обчислення біноміальних розподілів, використовуваних при статистичній інтерференції. Біноміальний розподіл, також відомий як випробування Бернуллі, має два типи успіху p і невдачу S. Основна мета моделі біноміального розподілу полягає в тому, щоб обчислити можливі результати ймовірності шляхом моніторингу конкретної кількості позитивних можливостей шляхом повторення процесу певну кількість разів . Вони повинні мати два можливі результати (успіх / невдача), тому результат є двобічним. Заздалегідь визначені математичні позначення p = успіх, q = 1-p.
Існують чотири функції, пов'язані з біноміальними розподілами. Вони є dbinom, pbinom, qbinom, rbinom. Форматований синтаксис наведено нижче:
Синтаксис
- dbinom (x, розмір, prob)
- pbinom (x, розмір, prob)
- qbinom (x, розмір, prob) або qbinom (x, size, prob, lower_tail, log_p)
- rbinom (x, розмір, prob)
У функції є три аргументи: значення x - вектор квантилів (від 0 до n), розмір - кількість спроб стежок, задача позначає ймовірність для кожної спроби. Давайте подивимось по черзі на прикладі.
1) dbinom ()
Це функція щільності або розподілу. Значення вектора повинно бути цілим числом, не повинно бути від’ємним числом. Ця функція намагається знайти ряд успіхів у «ні». випробувань, які фіксуються.
Біноміальний розподіл приймає величини та значення x. наприклад, розмір = 6, можливі значення х становлять 0, 1, 2, 3, 4, 5, 6, з чого випливає P (X = x).
n <- 6; p<- 0.6; x <- 0:n
dbinom(x, n, p)
Вихід:
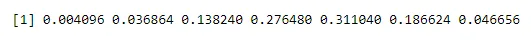
Складання ймовірності до одиниці
n <- 6; p<- 0.6; x <- 0:n
sum(dbinom(x, n, p))
Вихід:
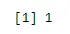
Приклад 1 - Лікарняна база даних показує, що пацієнти, які страждають на рак, від них помирають 65%. Яка ймовірність того, що 5 випадково обраних пацієнтів, з яких 3 видужають?
Тут ми застосуємо функцію dbinom. Ймовірність того, що 3 відновиться, використовуючи розподіл щільності у всіх точках.
n = 5, p = 0, 65, x = 3
dbinom(3, size=5, prob=0.65)
Вихід:

Для значення x від 0 до 3:
dbinom(0, size=5, prob=0.65) +
+ dbinom(1, size=5, prob=0.65) +
+ dbinom(2, size=5, prob=0.65) +
+ dbinom(3, size=5, prob=0.65)
Вихід:
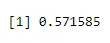
Далі створіть вибірку з 40 паперів і збільшуючи на 2, також створюючи двочлен, використовуючи dbinom.
a <- seq(0, 40, by = 2)
b <- dbinom(a, 40, 0.4)
plot(a, b)
Після виконання вищевказаного коду він дає наступний вихід: Біноміальний розподіл побудований за допомогою функції plot ().
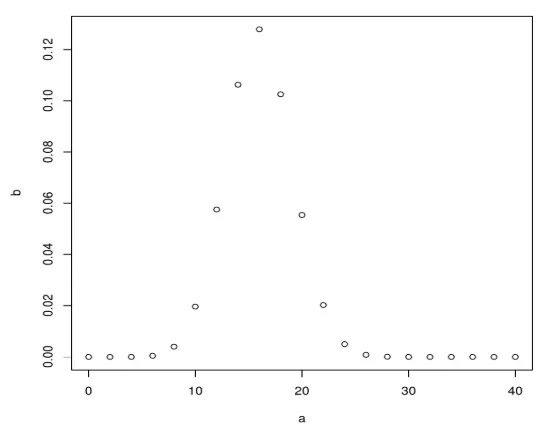
Приклад 2 - Розглянемо сценарій, припустимо, ймовірність того, що студент позичає книгу з бібліотеки, дорівнює 0, 7. У бібліотеці 6 учнів, яка ймовірність того, що 3 з них позичать книгу?
тут P (X = 3)
Код:
n=3; p=.7; x=0:n; prob=dbinom(x, n, p);
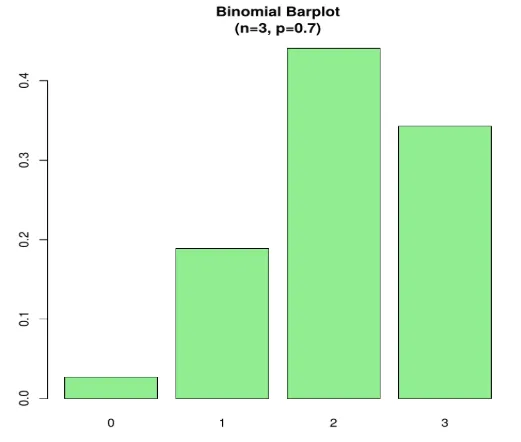
barplot(prob, names.arg = x, main="Binomial Barplot\n(n=3, p=0.7)", col="lightgreen")
Нижче графік показує, коли p> 0, 5, тому біноміальний розподіл позитивно перекошений, як показано.
Вихід:
2) Пбіном ()
обчислює кумулятивні ймовірності біноміального або CDF (P (X <= x)).
Приклад 1:
x <- c(0, 2, 5, 7, 8, 12, 13)
pbinom(x, size=20, prob=.2)
Вихід:

Приклад 2: Дравід забиває хвіртку на 20% своїх спроб, коли він мискує. Якщо він поклониться 5 разів, яка ймовірність, що він набере 4 або менше калитки?
Імовірність успіху тут становить 0, 2, і протягом 5 спроб ми отримуємо
pbinom(4, size=5, prob=.2)
Вихід:
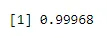
Приклад 3: 4% американців - чорні. Знайдіть ймовірність 2 чорношкірих студентів при випадковому виборі 6 учнів із 100 класу без заміни.
Коли R: x = 4 R: n = 6 R: p = 0. 0 4
pbinom(4, 6, 0.04)
Вихід: -
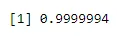
3) qbinom ()
Це квантільна функція і робить зворотну функцію сукупної ймовірності. Сукупне значення збігається зі значенням ймовірності.
Приклад: Скільки хвостів матимуть ймовірність 0, 2, коли монета буде кинута 61 раз.
a <- qbinom(0.2, 61, 1/2)
print(a)
Вихід: -
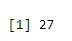
4) rbinom ()
Він генерує випадкові числа. Різні результати дають різний випадковий вихід, який використовується в процесі моделювання.
Приклад: -
rbinom(30, 5, 0.5)
rbinom(30, 5, 0.5)
Вихід: -

Кожен раз, коли ми виконуємо це, дає випадкові результати.
rbinom(200, 4, 0.4)
Вихід: -

Ось ми це робимо, припускаючи результат 30 перевернень монети за одну спробу.
rbinom(30, 1, 0.5)
Вихід: -
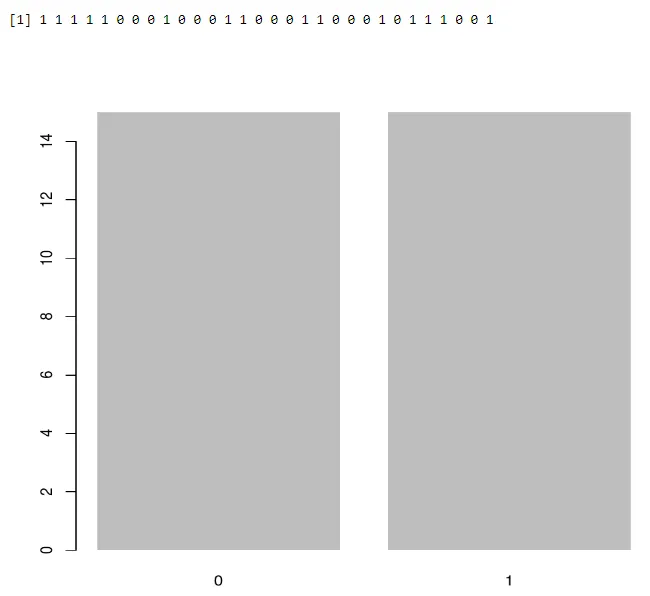
Використання барплоту:
a<-rbinom(30, 1, 0.5)
print(a)
barplot(table(a),>
Вихід: -
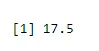
Щоб знайти середину успіху
output <-rbinom(10, size=60, 0.3)
mean(output)
Вихід: -
Висновок - Біноміальний розподіл у R
Отже, в цьому документі ми обговорили розподіл біномів у Р. Ми змоделювали, використовуючи різні приклади в фрагментах R studio та R, а також описали вбудовані функції, що допомагають генерувати біноміальні обчислення. Розрахунок біноміального розподілу в R використовує статистичні обчислення. Тому біноміальний розподіл допомагає знайти ймовірність та випадковий пошук за допомогою біноміальної змінної.
Рекомендовані статті
Це посібник щодо біноміального розподілу в Р. Тут ми обговорили вступ та його функції, пов'язані з розподілом біномів, разом із синтаксисом та відповідними прикладами. Ви також можете ознайомитися з іншими запропонованими нами статтями, щоб дізнатися більше -
- Формула біноміального розподілу
- Економіка проти бізнесу
- Методи бізнес-аналітики
- Linux дистрибутиви