Коефіцієнт формули визначення - Розрахунок за допомогою шаблону Excel

Коефіцієнт формули визначення (зміст)

Формула
Приклади

Що таке коефіцієнт формули визначення?

У статистиці коефіцієнт детермінації, який також називають R ^2, є інструментом, який визначає та оцінює здатність статистичної моделі пояснювати та прогнозувати майбутні результати. Іншими словами, якщо ми маємо залежну змінну y та незалежну змінну x у моделі, то R ² допомагає визначити варіацію y за варіацією x. Це один з ключових результатів регресійного аналізу і використовується тоді, коли ми хочемо передбачити майбутнє або протестувати деякі моделі із супутньою інформацією. Значення R ² лежить між 0 і 1 і вище значення R ², тим краще буде прогнозування і сила моделі. R ² дуже схожий на коефіцієнт кореляції, оскільки коефіцієнт кореляції вимірює пряму асоціацію двох змінних. R ² - це в основному квадрат коефіцієнта кореляції.

Формула для коефіцієнта визначення:

Існує кілька формул для обчислення коефіцієнта визначення:

Використання коефіцієнта кореляції:

Correlation Coefficient = Σ ((X – X _m ) * (Y – Y _m )) / √ (Σ (X – X _m ) ² * Σ (Y – Y _m ) ² )

Де:

X - Точки даних у наборі даних X
Y - Точки даних у наборі даних Y
X _m - середнє значення набору даних X
Y _m - середнє значення набору даних Y

Так

Coefficient of Determination(R ² ) = (Correlation Coefficient) ²

Використання регресійних виходів

Коефіцієнт детермінації (R ² ) = Пояснення варіації / Сумарна варіація

Коефіцієнт визначення (R ² ) = MSS / TSS

Coefficient of Determination (R ² ) = (TSS – RSS) / TSS

Де:

TSS - Загальна сума квадратів = Σ (Yi - Ym) ²
MSS - Модель Суми квадратів = Σ (Y - Ym) ²
RSS - Залишкова сума квадратів = Σ (Yi - Y ^) ²

Y - передбачуване значення моделі, Yi - значення i, а Ym - середнє значення

Приклади коефіцієнта формули визначення (із шаблоном Excel)

Візьмемо приклад, щоб краще зрозуміти обчислення коефіцієнта визначення.

Ви можете завантажити цей коефіцієнт шаблону формули Excel формули визначення тут - коефіцієнт шаблону формули визначення формули Excel

Коефіцієнт формули визначення - приклад №1

Скажімо, у нас є два набори даних X&Y і кожен містить 20 випадкових точок даних. Обчисліть коефіцієнт визначення для набору даних X & Y.

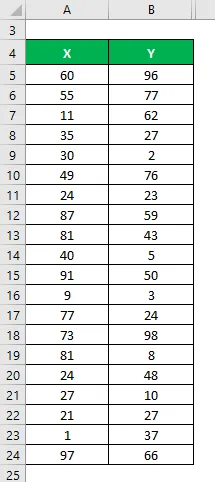
Середнє значення обчислюється як:

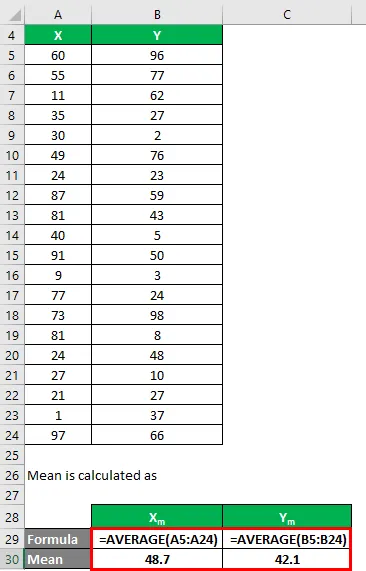
Середнє значення набору даних X = 48, 7
Середнє значення набору даних Y = 42, 1

Тепер нам потрібно обчислити різницю між точками даних та середнім значенням.

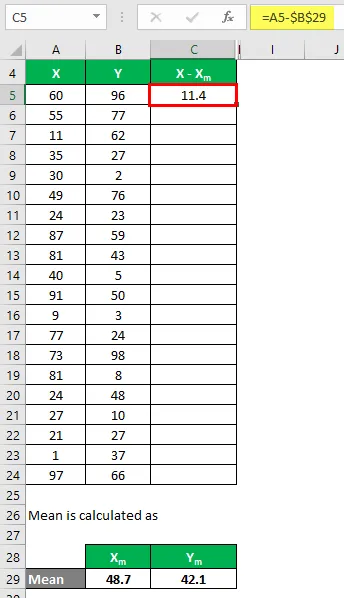
Аналогічно обчисліть для всіх наборів даних X.

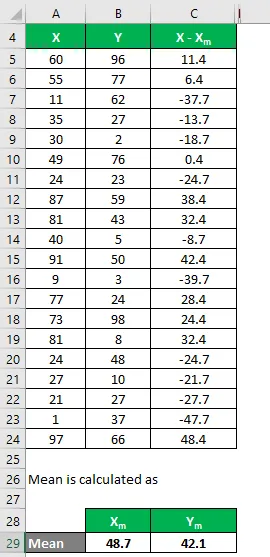
Аналогічно обчисліть його і для набору даних Y.

Обчисліть квадрат різниці для обох наборів даних X і Y.

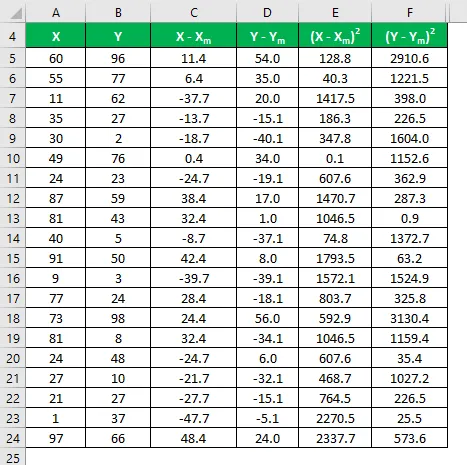
Помножте різницю X на Y.

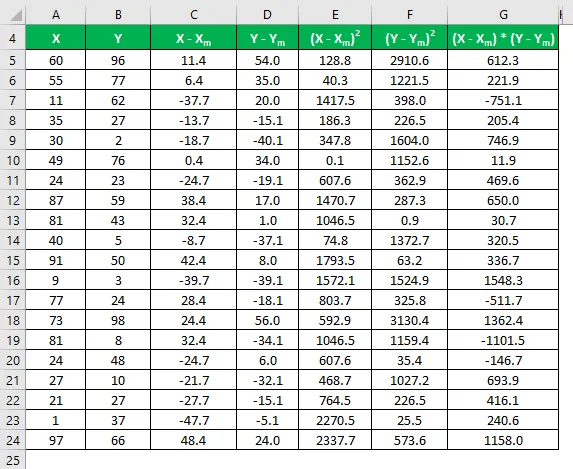
Коефіцієнт кореляції розраховується за формулою, наведеною нижче

Коефіцієнт кореляції = Σ ((X - X _m ) * (Y - Y _m )) / √ (Σ (X - X _m ) ² * Σ (Y - Y _m ) ² )

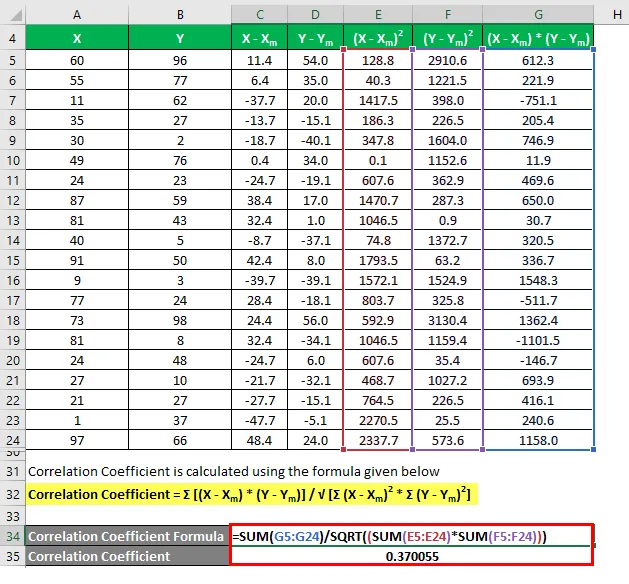
Коефіцієнт визначення визначається за формулою, наведеною нижче

Коефіцієнт детермінації = (коефіцієнт кореляції) ²

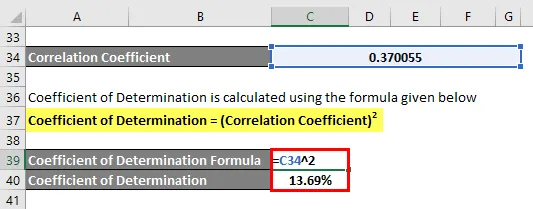
Коефіцієнт визначення = 13, 69%

Коефіцієнт формули визначення - приклад №2

Скажімо, ви дуже ризикований інвестор і хочете вкласти гроші на фондовому ринку. Ви не впевнені, в які акції інвестувати, а також апетит до ризику низький. Таким чином, ви хочете інвестувати в безпечний запас, який може імітувати показник. Ваш друг, який є активним інвестором, увійшов до списку 3 акцій для вас, виходячи з їх основної та технічної інформації, і ви хочете вибрати 2 акції серед цих трьох.

Ви також збирали інформацію про їх історичні прибутки за останні 15 років.

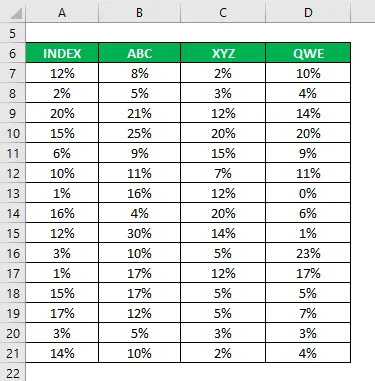
Коефіцієнт кореляції розраховується за формулою excel

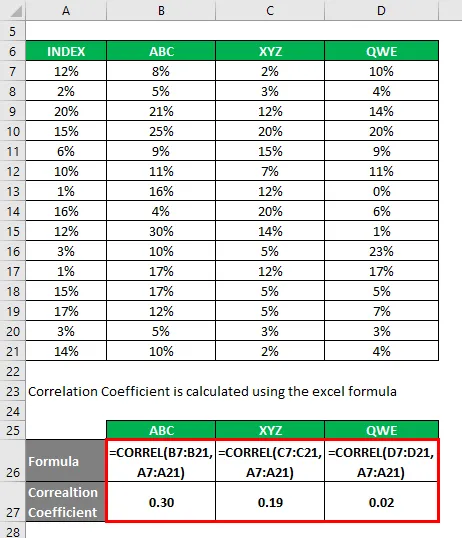
Коефіцієнт визначення визначається за формулою, наведеною нижче

Коефіцієнт детермінації = (коефіцієнт кореляції) ²

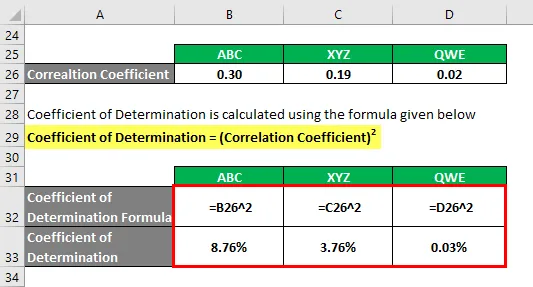
Виходячи з інформації, ви виберете акції ABC та XYZ для інвестування, оскільки вони мають найвищий коефіцієнт визначення.

Пояснення

Коефіцієнт визначення, як пояснено вище, - квадрат кореляції між двома наборами даних. Якщо R ² дорівнює 0, це означає, що немає кореляції і незалежна змінна не може передбачити значення залежної змінної. Аналогічно, якщо його значення дорівнює 1, це означає, що незалежна змінна завжди буде успішною в прогнозуванні залежної змінної. Але є і деякі обмеження. Хоча це говорить нам про співвідношення між двома наборами даних, воно не говорить про те, чи достатньо цього значення чи ні.

Крім того, велике значення R ² не завжди означає, що дві змінні мають міцні взаємозв'язки і це може бути потік. Наприклад: Скажімо, вартість R ² між кількістю автомобілів, проданих за рік, і кількістю ящиків морозива, проданих за рік, становить 80%. Але між цими двома відносинами немає. Тож слід бути дуже обережним під час використання R ² та спершу зрозуміти дані, а потім застосувати метод

Актуальність та використання коефіцієнта формули визначення

Існує багато практичних застосувань R ² . Наприклад, R2 дуже часто використовується інвесторами для порівняння продуктивності свого портфеля з ринком і намагається також передбачити майбутні напрями. Аналогічно, хедж-фонди, які використовують R ^2, допомагають їм моделювати ризик у своїх моделях. Але врешті-решт результат базується на чистих цифрах та статистиці, які іноді можуть вводити в оману. Як було сказано вище, спочатку потрібно перевірити, чи має вихід R ² сенс у реальному житті чи ні.