✅ AVL дерево в структурі даних - 3 найкращих операції, виконані на дереві AVL

Вступ до дерева AVL в структурі даних

Вступ до дерева AVL в структурі даних

Дерево AVL у структурі даних відноситься до дерева Адельсона, Вельського та Ландіса. Це вдосконалена версія дерева двійкового пошуку. Він має всі функції як у двійкового дерева пошуку, але відрізняється лише тим, що вони підтримують різницю між висотою лівого піддерева та правого піддерева, а також запевняють, що його значення на дереві становить <= 1, це відомо як Баланс Фактор.

Balance Factor = height(left-subtree) − height(right-subtree)

Наприклад: Розгляньте такі дерева

У наведеному вище прикладі висота правого піддерева = 2 і лівого = 3, таким чином BF = 2, тобто <= 1, таким чином, дерево, як вважається, врівноважене.

Навіщо нам потрібне дерево AVL в DS?

Працюючи з деревом бінарного пошуку, ми стикаємося зі сценарієм, в якому елементи впорядковані. У таких випадках усі елементи масиву розташовані на одній стороні кореня, це призводить до збільшення часової складності пошуку елемента в масиві, а складність стає O (n), тобто найгірша складність дерева . Щоб вирішити такі проблеми та скоротити час пошуку, дерева AVL були винайдені Adelson, Velski & Landis.

Приклад:

На наведеному малюнку висота лівого піддерева = 3 була такою ж

Висота правого піддерева = 0

Таким чином, коефіцієнт балансу = 3-0 = 3. Таким чином, пошук елемента в такому дереві має складність O (n), подібну до лінійного пошуку. Щоб уникнути цього складного пошуку AVL дерево було введено там, де потрібно підтримувати кожен вузол дерева

коефіцієнт балансу <= 1, інакше для виконання балансу такого дерева слід застосовувати різні методи повороту.

Struct AVLNode ( int data; struct AVLNode *left, *right; int ball factor; );

Типи обертань

Коли коефіцієнт балансу для дерева не задовольняє <= 1 умові, тоді на них потрібно здійснити обертання, щоб перетворити його на збалансоване дерево.

Існує 4 типи обертів:

1. Обертання ліворуч: Якщо додавання вузла праворуч від дерева приводить до дисбалансу, то в цьому випадку потрібно виконати обертання ліворуч.

2. Правий поворот: Якщо додавання вузла зліва від дерева призводить до дисбалансу вузла, потрібно здійснити Праве обертання. Іншими словами, Коли кількість ліній збільшується з лівого боку, то виникає потреба змістити елементи в праву сторону, щоб збалансувати її, таким чином, це називається правим обертанням.

3. Обертання вліво-вправо: Цей тип обертання є комбінацією вищеописаних двох обертів. Цей тип обертання відбувається, коли один елемент додається до правого піддерева лівого дерева.

У такому випадку спочатку виконайте обертання ліворуч на піддереві, а потім праворуч обертання лівого дерева.

4. Обертання вправо-вліво: Цей тип обертання також складається з послідовності вище двох обертів. Цей тип обертання потрібен, коли елемент додається зліва від правого піддерева і дерево стає незбалансованим. У такому випадку ми спочатку виконуємо правильне обертання на правому піддереві, а потім ліве обертання на правому дереві.

Операції на дереві AVL в DS

Нижче 3 операції, які можна виконати на дереві AVL:

1. Пошук

Ця операція схожа на пошук в Binary Search Tree. Наступні кроки наведені нижче:

Прочитайте елемент, наданий користувачем, сказати x.
Порівняйте елемент із кореня, якщо він однаковий, тоді вийдіть інакше перейдіть до наступного кроку.
Якщо х

Ще йдіть до потрібної дитини і порівняйте ще раз.

Дотримуйтесь процесів B і C, поки не знайдете елемент і вийдете.

Цей процес має складність O (log n).

Приклад:

	Розглянемо це Дерево, де нам потрібно здійснити пошук значення вузла 9. По-перше, нехай x = 9, значення кореня (12)> x, тоді значення повинно бути в лівому піддереві кореневого елемента.
	Тепер x порівнюється зі значенням вузла 3 x> 3, таким чином, ми повинні рухатися до правого піддерева.
	Тепер x порівнюється з вузлом (9), де 9 == 9 повертає істину. Таким чином, пошук елементів завершується в дереві.

2. Вставка

Вставляючи елемент у дерево AVL, нам потрібно знайти конкретний елемент розташування, який потрібно вставити, а потім елемент приєднати так само, як і вставку в BST, але після цього перевіряється, чи дерево все ще врівноважене чи ні тобто коефіцієнт балансу вузла дорівнює <= 1. А конкретні обертання виконуються за потребою.

Складність - O (log n).
Приклад. Розглянемо дерево нижче,

	Кожен вузол має коефіцієнт балансу, оскільки 0, -1 або 1, таким чином дерево збалансовано. Тепер розповімо, що відбувається, коли вставляється вузол зі значенням 1. Перше дерево об’їжджається, щоб знайти місце, де його потрібно вставити… 1 <2 таким чином записується як ліва дочірка вузла (2).
	Після вставки вузол (9) стає незбалансованим з коефіцієнтом балансу = 2. Тепер він піддається правильному обертанню.
	Дерево набуває рівноваги після правого обертання, і таким чином операція вставки успішно завершена.

3. Видалення

Видалення елемента в дереві AVL також включає пошук елемента в дереві та його видалення. Операція пошуку така ж, як і BST, і після знаходження елемента, який потрібно видалити, елемент видаляється з дерева і елементи коригуються, щоб зробити його знову BST. Після перевірки цих елементів є коефіцієнт балансу 0, -1 або 1, і, таким чином, виконуються відповідні обертання, щоб зробити його збалансованим.

Складність, якщо O (log n).

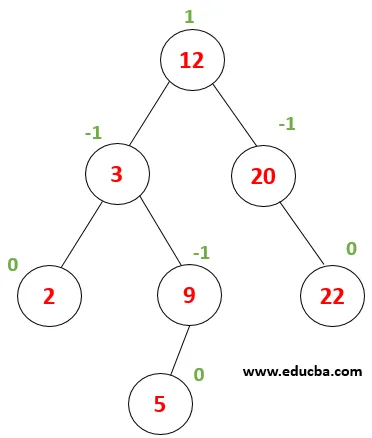
	Розглянемо дане дерево, всі з яких мають коефіцієнт балансу 0, -1 або 1. Тепер видалимо вузол зі значенням 16. Перше дерево проходить для пошуку вузла зі значенням 16, аналогічного алгоритму пошуку.
	Вузол 16 буде замінено попереднім попередником цього вузла, який є найбільшим елементом з лівого піддерева, тобто 12 Дерево стало незбалансованим, тому LL - необхідно здійснити поворот.
	Тепер кожен вузол став врівноваженим.

Висновок - дерево AVL в структурі даних

Дерево AVL є нащадком бінарного дерева пошуку, але долає його недолік, що збільшує складність у випадку сортування елементів. Він контролює коефіцієнт балансу дерева, який буде 0 або 1 або -1. У випадку, якщо воно стає незбалансованим, відповідні методи обертання виконуються для балансування дерева.

AVL дерево в структурі даних - 3 найкращих операції, виконані на дереві AVL