✅ Z Оцінка формули - Калькулятор (приклади з шаблоном Excel)

Що таке формула показника Z?

Формула показника Z (Зміст)

Формула
Приклади
Калькулятор

Що таке формула показника Z?

"Оцінка Z" - це один із найбільш широко використовуваних статистичних інструментів, який використовується для стандартизації балів за умови сукупності засобів та стандартного відхилення. Таким чином, оцінка Z також відома як стандартна оцінка. Оцінка Z змінюється в діапазоні від -3 рази від стандартного відхилення до +3 разів більше від стандартного відхилення із середнім нулем і середнього відхилення. Формула Z бала змінної може бути отримана шляхом вирахування середнього значення сукупності з даної змінної (яка є частиною набору даних чи сукупності), а потім діленням результату на стандартне відхилення сукупності. Математично він представлений як,

Z = (X – μ) / σ

де,

X = змінний від сукупності
μ = середня кількість населення
σ = Стандартне відхилення сукупності

Приклади формули показника Z (із шаблоном Excel)

Візьмемо приклад, щоб краще зрозуміти обчислення показника Z.

Ви можете завантажити шаблон шаблону формули Ex Score тут - Шаблон Z Score Formula Excel

Z Оцінка формули - приклад №1

Візьмемо для прикладу Менні, який нещодавно виступав на SAT. Йому вдалося забити 1109 у цій спробі. Однак, згідно з наявною інформацією, середній бал за SAT залишався близько 1030 при стандартному відхиленні 250. Обчисліть бал Z для оцінки Метні SAT та оцініть, наскільки він добре зробив порівняно із середніми тестувальниками.

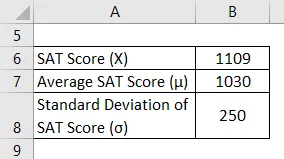
Рішення:

Z Оцінка розраховується за формулою, наведеною нижче

Z = (X - μ) / σ

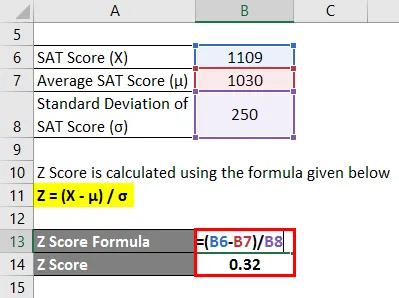
Z бал = (1109 - 1030) / 250
Z Оцінка = 0, 32

Таким чином, показник SAT Менні на 0, 32 стандартного відхилення вищий за середній бал учасників тестування, що свідчить про те, що 62, 55% учасників тестування набрали менше, ніж Менні.

Z Оцінка формули - приклад №2

Тепер візьмемо для прикладу Челсі, яка двічі написала САТ і хоче порівняти її виступ у них. У першій та другій спробах їй вдалося забити 1085 та 1059 відповідно. Згідно з наявною інформацією, середня оцінка та стандартне відхилення під час першої спроби склали відповідно 1100 та 230, тоді як в останній - 1050 та 240 відповідно. Допоможіть, будь ласка, "Челсі" вирішити, на якому іспиті вона виконала краще.

Рішення:

1-а спроба

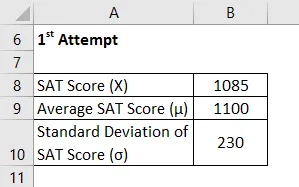
Z Оцінка розраховується за формулою, наведеною нижче

Z = (X - μ) / σ

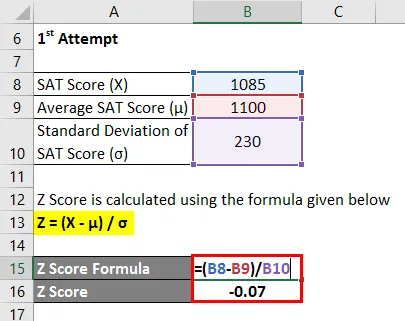
Z оцінка = (1085 - 1100) / 230
Z бал = -0, 07

Таким чином, показник SAT Челсі в першій спробі на 0, 07 стандартного відхилення нижчий за середній бал учасників тестів, що вказує на те, що 47, 40% тих, хто приймав тести, набрав менше, ніж "Челсі" під час першої спроби.

^Друга спроба

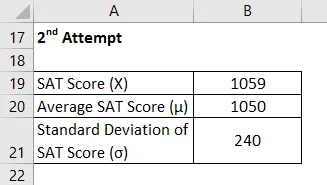
Z Оцінка розраховується за формулою, наведеною нижче

Z = (X - μ) / σ

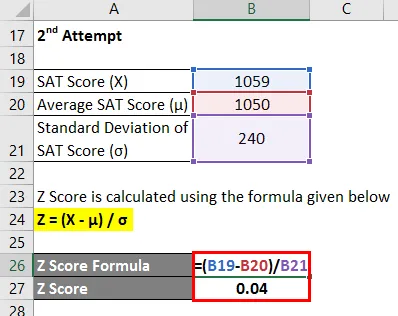
Z Оцінка = (1059 - 1050) / 240
Z бал = 0, 04

Таким чином, показник SAT Челсі у другій спробі на 0, 04 стандартного відхилення вищий за середній бал учасників тестів, що вказує на те, що 51, 50% тих, хто взяв тести, набрав менше, ніж Челсі під час ^другої спроби.

Тож із порівняння балів Z видно, що "Челсі" виступила краще під час своєї ^другої спроби.

Пояснення

Формула балу Z може бути отримана за допомогою наступних кроків:

Крок 1: По-перше, побудуйте сукупність з великою кількістю змінних, і змінні позначаються X _i .

Крок 2: Далі обчислюється кількість змінних у сукупності та позначається N.

Крок 3: Далі, середнє значення сукупності обчислюється шляхом підсумовування всіх змінних з подальшим поділом на загальну кількість змінних (крок 2) у наборі даних. Середнє значення популяції позначається μ.

μ = ∑ X _i / N

Крок 4: Далі вирахуйте середнє значення з кожної змінної набору даних, щоб обчислити їх відхилення від середнього.

тобто (X _i - μ) - відхилення для i- ^ї точки даних.

Крок 5: Далі обчисліть відхилення у квадраті для змінних, тобто (X _i - μ) ² .

Крок 6: Далі, складіть всі відхилення у квадраті, а потім розділіть загальну кількість на кількість змінних у наборі даних, щоб дійти до дисперсії.

σ ² = ∑ (X _i - μ) ² / N

Крок 7: Далі стандартне відхилення сукупності обчислюється обчисленням квадратного кореня дисперсії, обчисленої на вищенаведеному кроці.

σ = √ ∑ (X _i - μ) ² / N

Крок 8: Нарешті, формула оцінки Z виводиться шляхом вирахування середньої сукупності (етап 3) від змінної, а потім діленням результату на стандартне відхилення сукупності (етап 7), як показано нижче.

Z = (X - μ) / σ

Релевантність та використання формули Z-балу

З точки зору статистики, концепція показника Z є дуже важливою, оскільки корисна при визначенні ймовірності того, чи відбудеться подія в межах нормального розподілу. Насправді, бал Z також використовується для порівняння двох бальних результатів із двох різних нормальних розподілів, і це робиться шляхом перетворення необроблених балів у Z балів чи стандартизованих балів. Крім того, позитивний показник Z передбачає бал, який вищий за середнє, тоді як негативний показник Z передбачає бал менше середнього.

Z Оцінка формули калькулятор

Ви можете скористатися наступним калькулятором формул Z Score

Х
µ
σ
Z

Z =

X - µ
	=
σ

0-0
	=	0
0

Z Оцінка формули - Калькулятор (приклади з шаблоном Excel)

Що таке формула показника Z?