
Вступ до серії Фібоначчі в Python
Серія Фібоначчі в Python це називається рядом чисел, де наступне число - це сума цих двох чисел.
Наприклад:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 .. так далі
Тож тут 0 + 1 = 1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
8+ 13 = 21 тощо.
Дивлячись на вищесказане, можна було б мати певне уявлення про те, про що ми говоримо.
Однак, з точки зору математичного правила, його можна записати так:

Де n-е число - це сума числа в місцях (n-1) і (n-2). Що стосується реалізації серії Фібоначчі, то може бути кілька мов кодування, за допомогою яких це можна зробити.
Однак Python - широко поширена мова в наш час. Подивимось реалізацію серії Фібоначчі через Python. Слід знати про основні констатації обумовлення, такі як цикл, якщо не, а цикл тощо в Python, перш ніж продовжуватись тут. Якщо ні, то було б чудово, якщо можна переглядати його, а потім переймати вміст, що виходить. Тут для демонстраційних цілей я використовую шпідер, який є IDE для мови програмування python. Можна також використовувати будь-які інші ноутбуки IDE або Ipython, а також для виконання програм Python.
Серія Фібоначчі в Пітоні
Давайте подивимось реалізацію числа і рядів Фібоначчі, що враховують 1- й два елементи Фібоначчі - 0 і 1:
Однак ви можете налаштувати функцію Фібоначчі відповідно до вашої вимоги, але побачити основи спочатку та поступово переходити до інших.
Код Пітона для знаходження n-го числа Фібоначчі
Код 1:
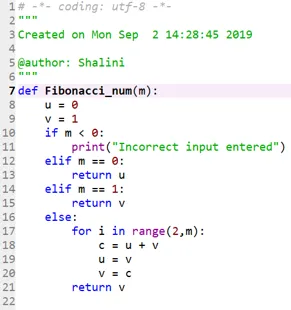
def Fibonacci_num(m):
u = 0
v = 1
if m < 0:
print("Incorrect input entered")
elif m == 0:
return u
elif m == 1:
return v
else:
for i in range(2, m):
c = u + v
u = v
v = c
return v
Код 2:
Вихід:
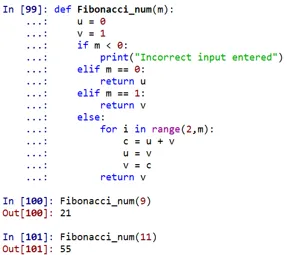
Як видно, число Фібоначчі на 9- му місці було б 21, а на 11- му - 55.
- Тут “Weight_num” - це визначена функція, яка дбає про знаходження числа Фібоначчі за допомогою певних умов. Цю функцію можна викликати, вказавши будь-яку позицію.
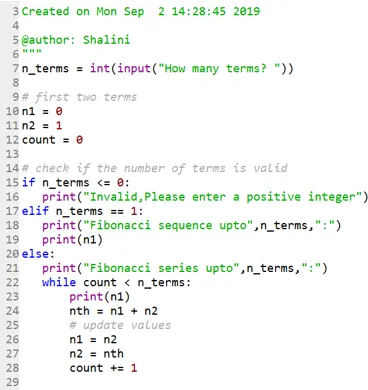
Тепер давайте подивимося, як можна друкувати серії до зазначеної позиції:
Код:
Вихід:
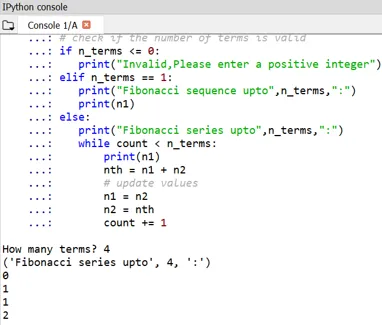
Можна помітити, що початок чисел Фібоначчі визначається як 0 і 1.
- Якщо хтось хоче визначити свої власні початкові умови, це також можна зробити так само, налаштувавши n1 і n2. Ось приклад для цього:
Скажімо, зараз ми хочемо, щоб нашими початковими умовами були: n1 = 3, n2 = 5
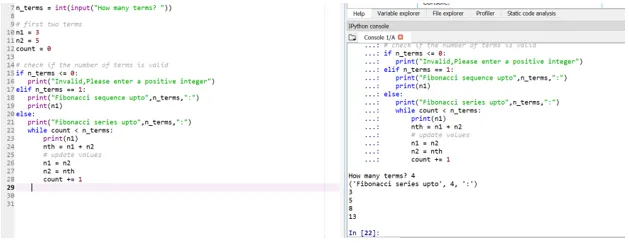
Тож тут ваша позиція на 4- му терміні (введений користувачем) буде визначатися виходячи з початкових умов.
Методи, за допомогою яких можна генерувати ряд Фібоначчі
Нижче наведено три методи, за допомогою яких можна генерувати ряд Фібоначчі:
1. Через генератори
Код:
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
Вихід:
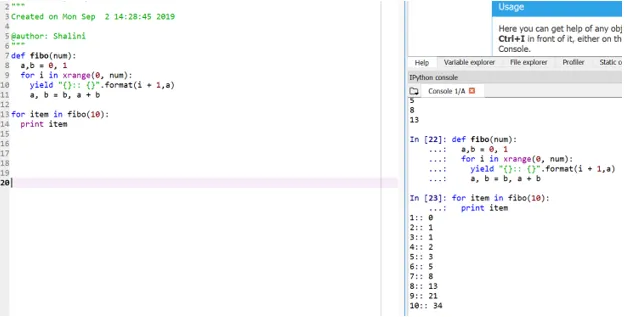
Цей метод називають "генератором", оскільки функція xrange є генератором чисел від 0 до числа, а вихід є генератором для відформатованого виводу.
Ось що робить xrange для вас:

Тут ряд Фібоначчі був визначений у формі функції, всередині якої для циклу, xrange та функції урожайності піклується про вихід.
2. Через петлю
Код:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
Вихід:

Як бачимо, для друку рядів Фібоначчі від 0 до 10. використовувались прості для циклу, що знаходяться між 0 і 10. Усередині циклу для змінних присвоюються нові значення. U і v - початкові значення за замовчуванням Фібоначчі, встановлені відповідно 0 і 1.
Що стосується прогресування циклу, то нове значення u - це старе значення v, тоді як нове значення v - це сума старих значень u і v. Це продовжується до кінця значень діапазону.
3. Через рекурсію
Код:
#Through recursion
def fibonacci_ser(m):
if(m <= 1):
return m
else:
return(fibonacci_ser(m-1) + fibonacci_ser(m-2))
m = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(m):
print fibonacci_ser(i),
Вихід:
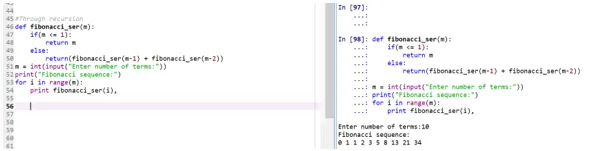
- Функція "alig_ser" робить дзвінок собі надрукувати серію Фібоначчі.
- Отже, метод отримав свою назву "рекурсія".
Тут виконуються кроки:
- Тут користувач попросив ввести місце, до якого потрібно надрукувати серію Фібоначчі.
- Число проходить через функцію "vred_ser".
- Умова перевіряється, якщо надана довжина менше 1 чи ні. Якщо так, результат дається негайно.
- Однак якщо довжина більша за 1, рекурсивні виклики проводяться до "fond_ser" з аргументами, що мають довжину менше 1 і 2, тобто.
- Отже, рекурсія дає бажаний вихід і друкує його.
- Отже, коротше, ми обговорили три способи відображення серії Фібоначчі.
- Через цикл, через генератори та через рекурсію.
Всі три Python Code узагальнені
Нижче наведено три пітонних коду:
1. Через генератори
Код:
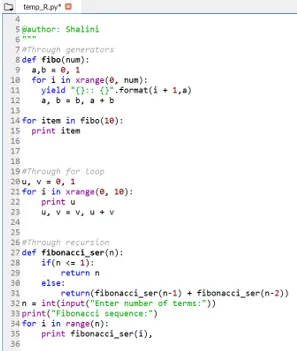
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
2. Через петлю
Код:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
3. Через рекурсію
Код:
def fibonacci_ser(n):
if(n <= 1):
return n
else:
return(fibonacci_ser(n-1) + fibonacci_ser(n-2))
n = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(n):
print fibonacci_ser(i),
Узагальнене вище - це всі процедури, потрібно практикуватись, щоб добре впоратися з усіма.
Вихід:
Висновок
Переглядаючи вищевказаний зміст Фібоначчі, можна було б зрозуміти чітке розуміння чисел і рядів Фібоначчі, спеціалізованих на пітоні. Одного разу вам стане комфортно з логікою серії Фібоначчі, генеруючи інший набір серій, робота з іншими числами та з різними методами тепер стане для вас перешкодою. Логічний підхід - єдиний спосіб досягти успіху в цьому.
Рекомендовані статті
Це посібник із серії Фібоначчі в Python. Тут ми обговорюємо числа і ряди Фібоначчі, спеціалізовані з python, генеруючи інший набір рядів, працюючи з іншими числами та з різними методами. Ви також можете ознайомитись з іншими нашими пов’язаними статтями, щоб дізнатися більше -
- Генератор випадкових чисел у Python
- Математичні функції в Python
- Факторський в Python
- Інкапсуляція в Python
- Серія Фібоначчі на Яві
- Особливості Python
- Факторна програма в JavaScript
- Генератор випадкових чисел у Matlab
- Генератор випадкових чисел у C #
- Інкапсуляція в JavaScript