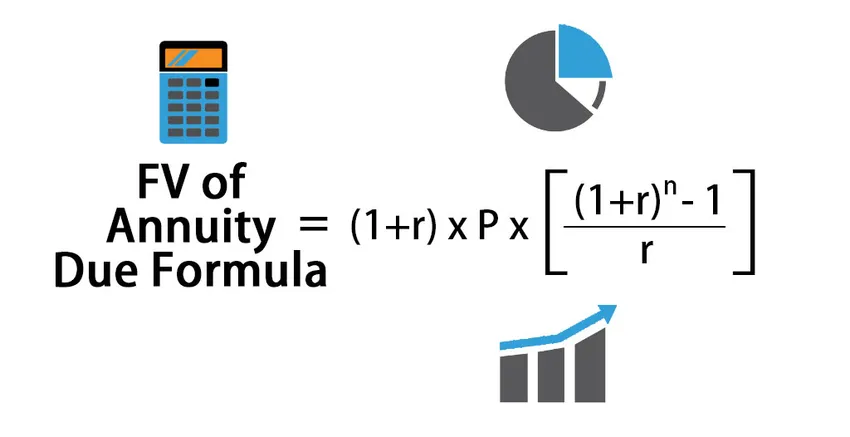
Майбутнє значення формули сплати ануїтету (Зміст)
- Майбутня вартість формули ануїтету
- Приклади майбутньої вартості формули належної ануїтету (із шаблоном Excel)
- Майбутнє значення калькулятора формули належної ануїтету
Майбутня вартість формули ануїтету
Формула для обчислення майбутньої вартості належної ануїтету:
FV of Annuity Due = (1+r) * P * (((1+r) n – 1) / r )
Де,
- P = Періодична оплата
- R = Норма за період
- N = Кількість періодів
Приклади майбутньої вартості формули належної ануїтету (із шаблоном Excel)
Візьмемо приклад, щоб краще зрозуміти підрахунок майбутньої вартості ануїтету.
Ви можете завантажити цей майбутні значення шаблону формули Excel Формула Excel тут - Майбутнє значення шаблону формули Excel формули ануїтетуПриклад №1
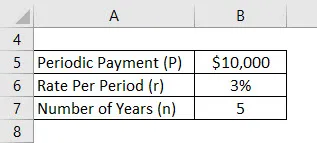
Припустимо, що Ананд депозитував 10 000 доларів на рік, а ефективна ставка, яку пропонує його рахунок, становить 3%. Тепер Ананд хоче порахувати свій майбутній баланс через 5 років, припускаючи перший депозит від сьогоднішнього дня.
Рішення:
Майбутня вартість належної ануїтету розраховується за формулою, наведеною нижче
FV з-за ануїтету = = (1 + r) * P * (((1 + r) n - 1) / r)
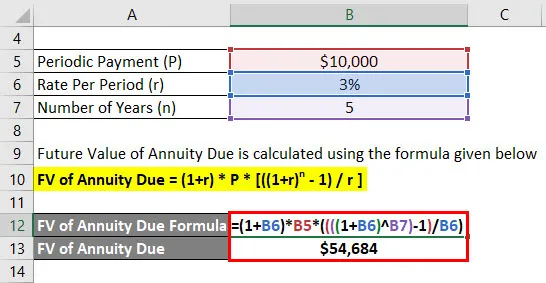
- FV ануїтету = = (1+ 3%) * 10 000 $ * (((((1 + 3%) 5) - 1) / 3%)
- ПВ з-за ануїтету = 54 684 доларів
Ананд отримає майбутній баланс 54 684 долари через 5 років.
Приклад №2
Припустимо, що Jagriti депозитував 8000 доларів на рік, а ефективна ставка, яку пропонує його рахунок, становить 5%. Тепер Джагріті хоче порахувати свій майбутній баланс через 5 років, припускаючи перший депозит від сьогоднішнього дня.

Рішення:
Майбутня вартість належної ануїтету розраховується за формулою, наведеною нижче
FV з-за ануїтету = = (1 + r) * P * (((1 + r) n - 1) / r)
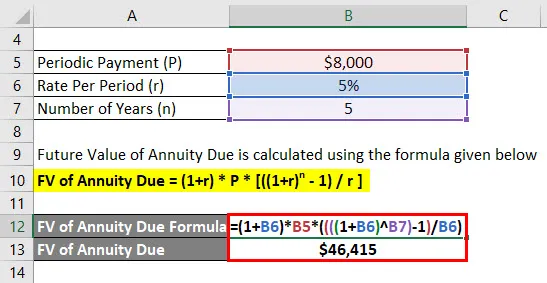
- FV ануїтету = = (1+ 5%) * 8000 $ * (((((1 + 5%) 5) - 1) / 5%)
- ПВ з ануїтету = 46 415 дол
Через 5 років Jagriti отримає $ 46 415 в майбутньому.
Приклад №3
Припустимо, що Анандріті здала 20 000 доларів на рік, а ефективна ставка, яку пропонує його рахунок, становить 2%. Тепер Анандріті хоче розрахувати свій майбутній баланс через 5 років, припускаючи перший депозит від сьогоднішнього дня.
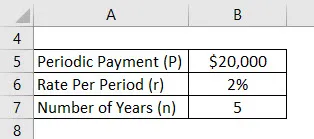
Рішення:
Майбутня вартість належної ануїтету розраховується за формулою, наведеною нижче
FV з-за ануїтету = = (1 + r) * P * (((1 + r) n - 1) / r)
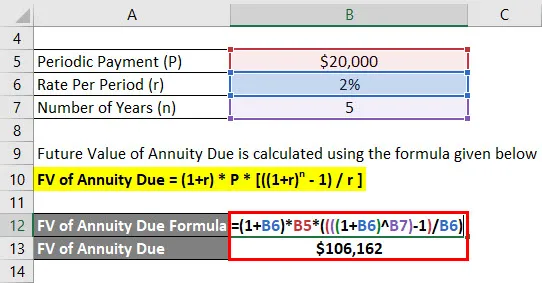
- FV ануїтету = = (1+ 2%) * $ 20 000 * (((((1 + 2%) 5) - 1) / 2%)
- ПВ з-за ануїтету = 1, 06, 162 дол
Анандріті отримає майбутній баланс 1, 06, 162 доларів через 5 років.
Пояснення
Для обчислення кінцевої вартості для серії грошових потоків або платежів, коли перший внесок отримується миттєво, ми використовуємо Майбутню вартість належної ануїтету. Перша миттєва розстрочка чи платіж розрізняють ануїтет через звичайну ануїтет. Безпосередня або миттєва ануїтет називається ануїтетом, що підлягає сплаті.
Він обчислює величину грошових потоків у майбутньому періоді. Використання ПДВ ануїтету в реальних ситуаціях відрізняється від теперішньої вартості ануїтету. Наприклад, припустимо, що компанія чи фізична особа купують ануїтет та сплатили перший внесок сьогодні. Ми можемо використовувати приклад, щоб пояснити далі, припустимо, що компанія або фізична особа хочуть купити ануїтет у будь-кого і здійснили перший платіж сьогодні. Для того, щоб розрахувати ціну, яку потрібно заплатити в цій ситуації, ми можемо використовувати теперішню формулу, обумовлену ануїтетом. Однак якщо ми хочемо обчислити залишок за рахунком після збереження відсотків за 5 років на рахунку, і ми вирішили сплатити перший внесок сьогодні, в цьому випадку використовується майбутня вартість ануїтету. Ануїтет, що належить до сплати, можна пояснити як тип ануїтету, коли грошові потоки відбуваються на початку кожного періоду. Через вдосконалений характер грошових потоків, кожен грошовий потік підлягає ефекту ущільнення протягом кожного додаткового періоду, якщо його порівнюють із звичайною ануїтет. Майбутня вартість звичайного ануїтету нижча, ніж майбутня вартість ануїтету, оскільки майбутня вартість ануїтету отримує періодичний відсоток від коефіцієнта один плюс.
Актуальність та використання майбутньої вартості належної ануїтету
Давайте розберемось у значенні майбутньої вартості та ануїтету, що належать окремо. Майбутня вартість може бути пояснена як загальна вартість суми грошових коштів, яка повинна бути виплачена в майбутньому на конкретну дату. А належна ануїтет може бути пояснена як серія платежів, яка проводиться на початку кожного періоду в регулярній послідовності. Отже, майбутня вартість належної ануїтету може бути пояснена як загальна вартість на визначену дату в майбутньому для серії систематичних / періодичних платежів, коли виплати здійснюються на початку кожного періоду. Цей вид трансакції та такий потік виплат можна побачити на рахунку бенефіціара пенсійного плану. Загальна вартість - це сума, до якої зростатиме ряд виплат, здійснених у майбутньому, оскільки передбачається певна сума відсотків, а прибуток поступово збільшується протягом певного періоду. Розрахунок майбутньої вартості звичайного ануїтету ідентичний цьому, але різниця полягає лише в тому, що ми додаємо додатковий період оплати, який проводиться на початку.
Майбутнє значення калькулятора формули належної ануїтету
Ви можете скористатися наступним калькулятором майбутньої вартості ануїтету
| П | |
| r | |
| н | |
| Майбутня вартість формули ануїтету | |
| Майбутня вартість формули ануїтету, що належить = | (1 + r) * P * (((1 + r) n - 1) / r) |
| = | (1 +0) * 0 * (((1 +0) 0 -1) / 0) = 0 |
Рекомендовані статті
Це було керівництвом щодо формули майбутньої вартості ануїтету. Тут ми обговорюємо, як розрахувати майбутню вартість ануїтету, а також практичні приклади. Ми також надаємо калькулятор майбутньої вартості ануїтету із завантажуваним шаблоном Excel. Ви також можете переглянути наступні статті, щоб дізнатися більше -
- Керівництво до формули вартості грошей у часі
- Приклади формули чинного фактору вартості
- Калькулятор формули співвідношення інформації
- Формула для ступеня операційного важеля