Формула помилки

Формула поля помилок (Зміст)

Формула помилки
Приклади формули резерву помилок (із шаблоном Excel)
Калькулятор формули помилок

У статистиці ми обчислюємо довірчий інтервал, щоб побачити, де значення даних вибіркової статистики впаде. Діапазон значень, що знаходяться нижче та вище вибіркової статистики в довірчому інтервалі, відомий як Похибка. Іншими словами, це в основному ступінь помилки в статистиці вибірки. Чим вище похибка, тим менше буде впевненість у результатах, оскільки ступінь відхилення в цих результатах дуже високий. Як випливає з назви, похибка - це діапазон значень вище та нижче фактичних результатів. Наприклад, якщо ми отримаємо відповідь в опитуванні, в якому 70% людей відповіли «добре», а помилка - 5%, це означає, що загалом від 65% до 75% населення вважають, що відповідь є «доброю» .

Формула для помилки -

Margin of Error = Z * S / √n

Де:

Z - Z оцінка
S - Стандартне відхилення населення
n - Розмір вибірки

Інша формула для обчислення похибки:

Margin of Error = Z * √((p * (1 – p)) / n)

Де:

p - вибіркова частка (частка успішної вибірки)

Тепер, щоб знайти бажаний z бал, потрібно знати інтервал довіри вибірки, оскільки оцінка Z залежить від цього. Нижче наведено таблицю, щоб побачити співвідношення довірчого інтервалу і z балів:

Довірчий інтервал	Z - оцінка
80%	1, 28
85%	1, 44
90%	1, 65
95%	1, 96
99%	2, 58

Після того, як ви знаєте інтервал довіри, ви можете використовувати відповідне значення z і обчислити звідти похибку.

Приклади формули резерву помилок (із шаблоном Excel)

Візьмемо приклад, щоб краще зрозуміти обчислення похибки.

Ви можете завантажити цей шаблон шаблону помилок тут - Поле шаблону помилок

Формула помилки - Приклад №1

Скажімо, ми проводимо опитування, щоб побачити, яку оцінку отримують студенти університету. Ми вибрали 500 учнів випадковим чином і запитали їх бал. Середнє значення - 2, 4 з 4, а стандартне відхилення - 30%. Припустимо, довірчий інтервал - 99%. Обчисліть похибку.

Рішення:

Похибка розраховується за формулою, наведеною нижче

Похибка = Z * S / √n

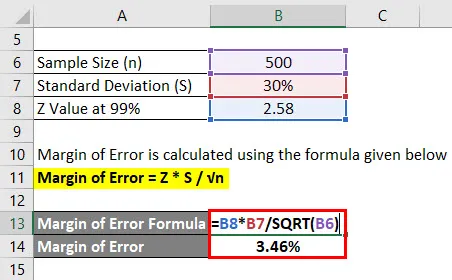
Похибка = 2, 58 * 30% / √ (500)
Похибка = 3, 46%

Це означає, що при 99% впевненості середній бал студентів становить 2, 4 плюс або мінус 3, 46%.

Формула помилки - Приклад №2

Скажімо, ви запускаєте на ринок новий медичний продукт, але вас бентежить, який аромат сподобається людям. Ви заплуталися між ароматом банану та ванільним ароматом і вирішили провести опитування. Ваше населення на це 500 000, що є вашим цільовим ринком, і з цього ви вирішили попросити думку 1000 людей, і це буде вибірка. Припустимо, що довірчий інтервал становить 90%. Обчисліть похибку.

Рішення:

Після того, як опитування зроблено, ви дізналися, що 470 людям сподобався аромат банана, а 530 просили аромат ванілі.

Похибка розраховується за формулою, наведеною нижче

Похибка = Z * √ ((p * (1 - p)) / n)

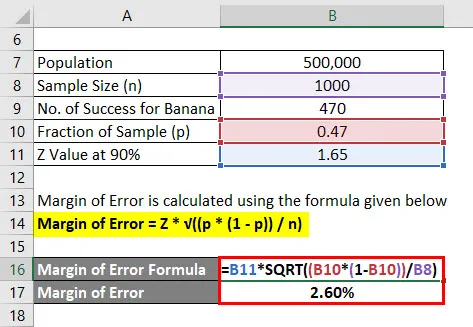
Похибка = 1, 65 * √ ((0, 47 * (1 - 0, 47)) / 1000)
Похибка = 2, 60%

Тож можна сказати, що з 90% впевненості, що 47% всіх людей любив банановий аромат плюс або мінус 2, 60%.

Пояснення

Як обговорювалося вище, помилка помилки допомагає нам зрозуміти, чи підходить вибіркова кількість вашого опитування чи ні. У випадку, якщо похибка маржі занадто велика, може статися так, що розмір вибірки занадто малий, і нам потрібно це збільшити, щоб результати вибірки більше відповідали результатам сукупності.

Є деякі сценарії, коли похибка не буде корисною і не допоможе нам відстежувати помилку:

Якщо питання опитування не розроблені і не допомагають отримати необхідну відповідь
Якщо люди, які відповідають на опитування, мають певні упередження щодо продукту, щодо якого проводиться опитування, то також результат не буде дуже точним
Якщо вибірка, обрана самим собою, є належним представником сукупності, то і в цьому випадку результати будуть відхилені.

Також одне велике припущення полягає в тому, що населення нормально розподілене. Тож якщо розмір вибірки занадто малий і розподіл населення не є нормальним, z оцінка не може бути обчислена, і ми не зможемо знайти межу помилки.

Релевантність та використання границь формули помилок

Кожного разу, коли ми використовуємо вибіркові дані, щоб знайти відповідну відповідь для сукупності населення, є певна невизначеність та шанси, що результат може відхилитися від реального результату. Похибка означає, що рівень відхилення є результатом вибірки. Нам потрібно мінімізувати похибку, щоб наші результати вибірки відображали фактичну історію даних про населення. Так що нижча похибка, тим краще будуть результати. Похибка доповнює та доповнює статистичну інформацію, яку ми маємо. Наприклад, якщо опитування виявить, що 48% людей вважають за краще проводити час вдома у вихідні, ми не можемо бути настільки точними, і в цій інформації є деякі відсутні елементи. Коли ми ввели сюди похибку, скажімо, 5%, то результат буде інтерпретовано, як 43-53% людям сподобалася ідея перебування вдома у вихідні, що має повний сенс.

Калькулятор формули помилок

Ви можете скористатися наступним калькулятором помилок

Z
S
√n
Помилка

Помилка

Z x	S	=

	√n

0 х	0	=	0

	0

Формула помилки - Калькулятор (шаблон Excel)

Зміст: